- 概率与统计
- 共1631题
甲、乙两人参加某种选拔测试,在备选的







(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率。
正确答案
见解析
解析
(1)解:设乙答题所得分数为






乙得分的分布列如下:

(2)解:由已知甲、乙至少答对


则

故甲乙两人至少有一人入选的概率
知识点
随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: 



(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为

正确答案
见解析。
解析
(1)由题意得,分数在

所以样本人数为


(2)从分组区间和频数可知,样本众数的估计值为
由(1)知分数在
所以频率分布直方图中
(3)成绩不低于80分的样本人数为4+2=6(人),成绩在90分以上(含90分)的人数为




所以
所以
知识点
从1,2,3,





正确答案
解析
略
知识点
福彩中心发行彩票的目的是为了获取资金资助福利事业,现在福彩中心准备发行一种面值为5元的福利彩票刮刮卡,设计方案如下:(1)该福利彩票中奖率为50%;(2)每张中奖彩票的中奖奖金有5元,50元和150元三种;(3)顾客购买一张彩票获得150元奖金的概率为

(1)假设某顾客一次性花10元购买两张彩票,求其至少有一张彩票中奖的概率;
(2)为了能够筹得资金资助福利事业, 求
正确答案
(1)0.75
(2)
解析
(1)设至少一张中奖为事件
则
(2) 设福彩中心卖出一张彩票可能获得的资金为
则


…………………8分
所以

所以当 

所以当
知识点
某大型公益活动从一所名牌大学的四个学院中选出了
(1)若从这
(2)现要从这




正确答案
见解析。
解析
(1)设“两名学生来自同一学院”为事件
则
即两名学生来自同一学院的概率为
(2) 







所以
…………………………………………………………………11分
所以
知识点
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高,现从一批数量很大的罗非鱼中随机地抽出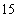
《中华人民共和国环境保护法》规定食品的汞含量不得超过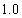
(1)检查人员从这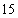
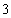
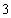
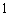
(2)若从这批数量很大的鱼中任选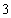
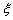
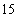
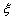

正确答案
见解析
解析
(1)记“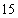
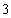
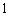
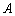
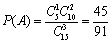
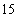
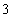
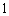
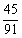
(2)依题意可知,这批罗非鱼中汞含量超标的鱼的概率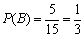
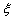
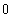
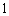
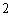
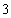
则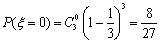
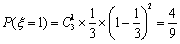
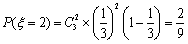
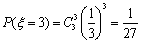
其分布列如下:
…………………………12分
所以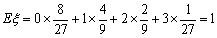
知识点
空气质量指数

甲、乙两城市2013年2月份中的15天对空气质量指数

(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(2)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(3) 在乙城市15个监测数据中任取


正确答案
见解析
解析
(1)甲城市空气质量总体较好. ………2分
(2)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为
乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为
在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率为
………8分
(3)




数学期望
知识点
某校高二年级进行社会实践,对[25, 55]岁的人群随机抽取n个人进行了一次是否开通“微信”, 若开通“微信”的为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图1所示统计表,如图2所示各年龄段人数频率分布直方图:
请完成以下问题:
(1)补全频率直方图,并求n,a,p的值;
(2)从[40,45)岁和[45,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络“时尚达人”大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁得人数为ξ,求ξ的分布列和数学期望E(X).
正确答案
见解析
解析
(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,所以高为
第一组的人数为
频率为0.04×5=0.2,所以
第四组的频率为0.03×5=0.15,人数为1000×0.15=150,
(2)因为[40,45)岁与[45,50)岁年龄段的“时尚族”的比值为60:30=2:1,所以分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,随机变量





数学期望为
知识点






(1)现有该班甲、乙、丙三名同学,求这

(2)若用

正确答案
见解析
解析
(1)设“这3名同学至少有2名同学收看发射直播”为事件
则
(2)由条件可知

即



知识点
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数字
(1)在一次试验中,求卡片上的数字为正数的概率;
(2)在四次试验中,求至少有两次卡片上的数字都为正数的概率;
(3)在两次试验中,记卡片上的数字分别为


正确答案
见解析
解析
(1)设事件A:在一次试验中,卡片上的数字为正数,则

答:在一次试验中,卡片上的数字为正数的概率是
(2)设事件B:在四次试验中,至少有两次卡片上的数字都为正数。
由(1)可知在一次试验中,卡片上的数字为正数的概率是
所以
答:在四次试验中,至少有两次卡片上的数字都为正数的概率为
(3)由题意可知,









所以随机变量
所以
知识点
某公司准备将100万元资金投入代理销售业务,现有A,B两个项目可供选择:
投资A项目一年后获得的利润X1(万元)的概率分布列如下表所示:
且X1的数学期望E(X1)=12;
投资B项目一年后获得的利润X2(万元)与B项目产品价格的调整有关, B项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p(0< p <1)和1p. 经专家测算评估:B项目产品价格一年内调整次数X(次)与X2的关系如下表所示:
(1)求a,b的值;
(2)求X2的分布列;
(3)若E(X1)< E(X2),则选择投资B项目,求此时 p的取值范围.
正确答案
(1)
(2)
(3)
解析
(1)由题意得:
解得:
(2)X2 的可能取值为



所以X2的分布列为:
……………………………………9分
(3)由(2)可得:

因为E(X1)< E(X2),
所以
所以
当选择投资B项目时,

知识点
某工厂在试验阶段大量生产一种零件,这种零件有甲、乙两项技术指标需要检测,设各项技术指标达标与否互不影响,按质量检验规定:两项技术指标都达标的零件为合格品,为估计各项技术的达标概率,现从中抽取1000个零件进行检验,发现两项技术指标都达标的有600个,而甲项技术指标不达标的有250个。
(1)求一个零件经过检测不为合格品的概率及乙项技术指标达标的概率;
(2)任意抽取该零件3个,求至少有一个合格品的概率;
(3)任意抽取该种零件4个,设ξ表示其中合格品的个数,求随机变量ξ的分布列。
正确答案
见解析。
解析
(1)记一个零件中甲项技术达标的事件为A,乙项技术达标的事件为B
由题意可得,两项技术都达标的概率为P(AB)=
甲项技术不达标的概率P(

因此一个零件经过检测不合格的概率为1﹣P(AB)=1﹣
由独立性可知,P(AB)=P(A)P(B)
∴P(B)=

即乙项技术指标达标的 概率为
(2)任意抽取该种零件3个,至少有一个合格品的概率1﹣
(3)随机变量ξ的可能取值为0,1,2,3,4
P(ξ=0)=
P(ξ=1)=
P(ξ=2)=
P(ξ=3)=
P(ξ=4)=
∴ξ的分布列为
知识点
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为


(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40个产品中任职2件,设

(3)从流水线上任取5件产品,估计其中恰有2件产品的重量超过505克的概率。
正确答案
见解析
解析
(1)重量超过505克的产品数量是
(2)




-------------------------------------------------------9分
(3)由(1)的统计数据知,抽取的40件产品中有12件产品的重量超过505克,其频率为



故所求的概率为
知识点
某学生在参加政、史、地三门课程的学业水平考试中,取得A等级的概率分别为


正确答案
解析
解:①学生在参加政、史、地三门课程的学业水平考试中,有两门取得A等级有以下3种情况:政、史;政、地;地、史。
∴P(ξ=2)=


②根据分布列的性质可得:P(ξ=1)=1﹣P(ξ=0)﹣P(ξ=2)﹣P(ξ=3)=

∴Eξ=0×



故答案为
知识点
甲、乙、丙三名优秀的大学毕业生参加一所重点中学的招聘面试,面试合格者可以签约。甲表示只要面试合格就签约,乙与丙则约定,两个面试都合格就一同签约,否则两人都不签约。设每个人面试合格的概率都是P,且面试是否合格互不影响。已知至少有1人面试合格概率为
(1)求P。
(2)求签约人数
正确答案
见解析。
解析
解:
(1)至少1人面试合格概率为


(2)签约人数

甲不合格,乙丙至少一人不合格



签约人数为0的概率:





签约人数为2的概率:甲不合格,乙丙全部合格:

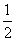
签约人数为3的概率:甲乙丙均合格:
分布表:
数学期望:
知识点
扫码查看完整答案与解析



































































