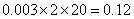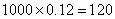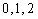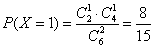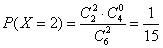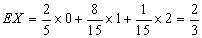- 概率与统计
- 共1631题
18. 现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为

(Ⅰ)求该射手恰好命中一次的概率;
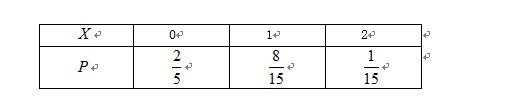
(Ⅱ)求该射手的总得分

正确答案
见解析
知识点
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得
19.根据以上资料完成下面的2×2列联表,若据此数据算得
20.以此“满意”的频率作为概率,求在3人中恰有2人满意的概率;
21.从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为

正确答案
(1)在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关;
解析
:(Ⅰ)
∵
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。
考查方向
解题思路
先将题中给出的茎叶图处理成列联表,然后带入求得
易错点
将茎叶图处理成列联表数据出错,
在求
正确答案
(2)
解析
(Ⅱ)由频率估计“满意”的概率为
∴在3人中恰有2人满意的概率为

考查方向
解题思路
先求出“满意”的概率,然后利用n次独立重复试验的概率求法求出概率;
易错点
求概率时忘记乘以
正确答案
(3)

数学期望
解析
(Ⅲ)





数学期望
考查方向
解题思路
先求出随机变量的取值和取各个值的概率后利用公式求出其期望。
易错点
不会求随机变量取各个值的概率。
以下茎叶图记录了甲、乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
19.如果X=8,求乙组同学植树棵树的平均数和方差。
20.如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
正确答案
解析
当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10。………2
所以平均数为
方差为
考查方向
解题思路
按题意直接求平均,按公式直接求方差
易错点
第(2)问随机变量找不准,对应有概率计算不准确。
正确答案
随机变量Y的分布列为:
数学期望19
解析
当X=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,11,11;
乙组同学的植树棵数是:9,8,9,10。
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,
这两名同学植树总棵数Y的可能取值为17,18,19,20,21。
事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”,
所以该事件有2种可能的结果,
因此P(Y=17)=
同理可得P(Y=18)=



所以,随机变量Y的分布列为:
EY=17×




考查方向
解题思路
统计事件总为4×4=16,总棵数Y的可能取值为17,18,19,20,21。算出概率,列分布列,直接求数学期望
易错点
第(2)问随机变量找不准,对应有概率计算不准确。
随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了了解公众对“延迟退休”的态度,某校课外研究性学习小组对公务员和教师各抽取了50人进行调查,将调查情况进行整理后制成下表:
19.求上表中
20.现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为X,求X的分布列和期望.
正确答案
m=10,n=30, p=30有95%的把握认为“是否同意延迟退休与不同的职业有关.
解析
根据题中提供的数据计算得
所以有95%的把握认为“是否同意延迟退休与不同的职业有关”
考查方向
解题思路
根据列联表的特点,直接求出m=10,n=30,p=30 o;利用公式求出卡方,
易错点
列联表中的原始数据,随机变量的取值及对应的概率
正确答案
所以X的分布列为
EX=1



解析
公务员有4人同意,1人不同意,教师有3人同意,2人不同意.从两个职业人群中各抽取2人,同意延迟退休的人数X的取值为1,2,3,4……………………6分



所以X的分布列为
EX=1



考查方向
解题思路
先统计公务员5个中同意与不同意的人数,再统计教师5中同意与不同意的人数,得到同意延迟退休的人数X的取值为1,2,3,4,然后算对应用的概率.
易错点
列联表中的原始数据,随机变量的取值及对应的概率
为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
17.从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为4
的概率?
18.若从阅读名著不少于4本的学生中任选4人,设选到的男学生人数为
量
19.试判断男学生阅读名著本数的方差

写出结论).
正确答案

解析
试题分析:本题属常见的概率问题,在审题时一要会识表,二要从题意中提炼数据列分布列计算概率和期望即可。其难度和其它概率问题一样难度适中,主要是题意的理解。
设事件
读本数之和为4 .
由题意可知, 
考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
从频数分布表读出数据再分析完成第一问得出结论。
找X,计算概率,列分布列,再计算期望。
易错点
第一问由频数分布表得出数据时易出错。第二、三问分布列中概率计算上易出错,再就是期望的计算也是学生易错点之一。
正确答案
EX=2;
解析
试题分析:本题属常见的概率问题,在审题时一要会识表,二要从题意中提炼数据列分布列计算概率和期望即可。其难度和其它概率问题一样难度适中,主要是题意的理解。
阅读名著不少于4本的学生共8人,其中男学生人数为4人,故

由题意可得




所以随机变量
随机变量

考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
从频数分布表读出数据再分析完成第一问得出结论。
找X,计算概率,列分布列,再计算期望。
易错点
第一问由频数分布表得出数据时易出错。第二、三问分布列中概率计算上易出错,再就是期望的计算也是学生易错点之一。
正确答案

解析
试题分析:本题属常见的概率问题,在审题时一要会识表,二要从题意中提炼数据列分布列计算概率和期望即可。其难度和其它概率问题一样难度适中,主要是题意的理解。
(Ⅲ)
考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
从频数分布表读出数据再分析完成第一问得出结论。
找X,计算概率,列分布列,再计算期望。
易错点
第一问由频数分布表得出数据时易出错。第二、三问分布列中概率计算上易出错,再就是期望的计算也是学生易错点之一。
某汽车公司为调查4S店个数对该
19.根据该统计数据进行分析,求y关于x的线性回归方程;
20.现要从A,B,E三座城市的9家4S店中选取4家做深入调查,求A城市中
被选中的4S店个数X的分布列和期望.
附:回归直线的斜率和截距的最小二乘法估计公式分
, .
正确答案
(1)
解析
(Ⅰ)




考查方向
解题思路
带公式求线性回归方程;
先找出随机变量的所有取值,分别求对应的概率并列出表格,然后到公式求出期望。
易错点
带公式求方程计算出错
分布列中随机变量求值及其概率求错
正确答案
(2)
解析






-------------9分

考查方向
解题思路
带公式求线性回归方程;
先找出随机变量的所有取值,分别求对应的概率并列出表格,然后到公式求出期望。
易错点
带公式求方程计算出错
分布列中随机变量求值及其概率求错
中国银行业监督管理委员会及其派出机构检查个人理财业务时,可以采用多样化的方式进行调查的事项有( )。
A.商业银行从事产品咨询、财务规划或投资顾问服务业务人员的专业胜任能力、操守情况,以及上述服务对投资者的保护情况
B.商业银行接受客户的委托和授权,按照与客户事先约定的投资计划和方式进行资产管理的业务活动,客户授权的充分性与合规性,操作程序的规范性
C.客户资产保管人员和账户操作人员职责的分离情况
D.商业银行销售和管理理财计划过程中对投资人的保护情况,以及对相关产品风险的控制情况
E.当期理财计划的收益分配和终止情况
正确答案
A,B,C,D
解析
[解析] 本题考查对个人理财业务的检查监管。选项E属于商业银行对个人理财业务的季度统计分析报告的内容,所以不选。
每逢节假日,在微信好友群发红包逐渐成为一种时尚,还能增进彼此的感情. 2016年春节期间,小鲁在自己的微信好友群中,向在线的甲、乙、丙、丁四位好友随机发放红包,发放的规则为:每次发放一个,每个人抢到的概率相同.
19.若小鲁随机发放了3个红包,求甲至少抢到一个红包的概率;
20.若丁因有事暂时离线一段时间,而小鲁在这段时间内共发放了3个红包,其中2个红包中各有10元,一个红包中有5元,记这段时间内乙所得红包的总钱数为

正确答案
设“甲至少得1红包”为事件
解析
考查方向
独立重复事件的概率
解题思路
教师点评
正确答案
由题意知







所以
解析
解题思路
教师点评
19.设某校新、老校区之间开车单程所需时间为


(1)求

(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
正确答案
19.(1)由统计结果可得T的频率分步为
以频率估计概率得T的分布列为
从而 
(2)设

解法一:

解法二:
故
解析
解析已在路上飞奔,马上就到!
知识点
20.某厂用鲜牛奶在某台设备上生产





该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利
(1)求
(2) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
正确答案
20.(1)设每天



目标函数为 
当

将

当



最大获利
当

将

当



最大获利
当
四个顶点分别为
将

当



最大获利
故最大获利
因此,
(2)由(1)知,一天最大获利超过10000元的概率
由二项分布,3天中至少有1天最大获利超过10000元的概率为
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
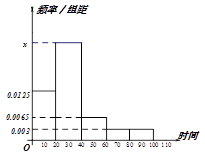
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是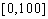
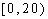
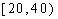
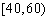
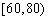
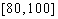
(1)求直方图中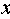
(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(3)现有6名上学路上时间小于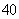
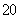
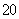
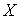
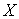
正确答案
见解析。
解析
(1)由直方图可得:
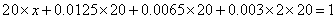
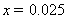
(2)新生上学所需时间不少于60分钟的频率为:
因为
所以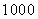
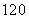
(3)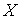
所以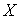
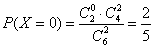
所以
知识点
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
[来源:学。科。网]
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在


正确答案
见解析
解析
知识点
在某批次的某种灯泡中,随机地抽取200个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
(1)根据频率分布表中的数据,写出a,b的值;
(2)某人从灯泡样品中随机地购买了
(3)某人从这个批次的灯泡中随机地购买了3个进行使用,若以上述频率作为概率,用X表示此人所购买的灯泡中次品的个数,求X的分布列和数学期望.
正确答案
见解析
解析
(1)解:

(2)解:由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,所以优等品、正品和次品的比例为



(3)解:


从本批次灯泡中购买3个,可看成3次独立重复试验,
所以



所以随机变量


(注:写出


知识点
10.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析