- 概率与统计
- 共1631题
已知暗箱中开始有3个红球,2个白球,现每次从暗箱中取出1个球后,再将此球和它同色的另外5个球一起放回箱中。
(1)求第2次取出白球的概率;
(2)若取出白球得2分,取出红球得3分,设连续取球2次的得分值为X,求X的分布列和数学期望。
正确答案
见解析。
解析
(1)第2次取出白球的事件包括:“第1次取出红球,第2将取出白球”记为事件A,“两次均取出白球”记为事件B,则A,B互斥,
P=P(A)+P(B)=

(2)X的所有可能取值为:4、5、6
P(X=4)=



P(X=6)=
于是
故E(X)=4×


知识点
已知身穿红.黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有 ( )
正确答案
解析
先把两个穿红衣服的人和穿蓝衣服的人排成一排,再用插空法把穿黄衣服的两人排入,有AA=72种排法,其中两个穿红衣服的人排在一起的排法有AAA=24种情况,则满足要求的排法共有72-24=48种
知识点
将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大,当3,4固定在图中的位置时,填写空格的方法数为
正确答案
解析
根据数的大小关系可知,1,2,9的位置是固定的,则剩余5,6,7,8四个数字,而8只能放在在A,B两个位置,若8放在B处,,则C处可以从5,6,7三个数字中选一个放在C处,剩余两个按照大小放在D,A处,此时共有3种,同理,若8放在A处,则可以从5,6,7三个数字中选一个放在D处,剩余两个按照大小放在B,C处,此时也有3种,所以共有6种填法,选A.
知识点
为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了200位老年人,结构如下:
参照附表,得到的正确结论是
正确答案
解析
由公式可计算


知识点
如图,


(1)写出信息总量
(2)求信息总量
正确答案
见解析
解析
(1)由已知,






(2)

知识点
将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大,当3,4固定在图中的位置时,填写空格的方法数为
正确答案
解析
根据数的大小关系可知,1,2,9的位置是固定的,
知识点
图是一容量为
正确答案
解析
根据中位数左右两侧的面积相等,也就是概率相等所以中位数为12,第一块的面积为

知识点
已知



正确答案
解析
本题为几何概率.区域



知识点
某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的,若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金,若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其它区域则不中奖(若指针停到两区间的实线处,则重新转动)。若顾客在一次消费中多次中奖,则对其奖励进行累加。已知顾客甲到该商场购物消费了268元,并按照规则能与了促销活动。
(1) 求顾客甲中一等奖的概率;
(2) 记

正确答案
见解析。
解析
(1) 设事件
所以该顾客中一等奖的概率是
(2)




所以
数学期望
知识点
某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[ 0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:
假设甲、乙两种酸奶独立销售且日销售量相互独立。
(1)写出频率分布直方图(甲)中的





(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设

正确答案
见解析
解析
(1)

(2)设事件
事件
事件


所以 


(3)由题意可知,




所以
………………11分
所以 

………………13分
另解:由题意可知
所以 

知识点
用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中有且只有两个偶数相邻,则这样的六位数的个数为 ( )
正确答案
解析
从2,4,6三个偶数中任意选出2个看作一个“整体”,方法有










知识点
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在


(1) 求该小区居民用电量的中位数与平均数;
(2) 利用分层抽样的方法从该小区内选出10位居民代表,若从该10户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率;
(3) 若该小区长期保持着这一用电消耗水平,电力部门为鼓励其节约用电,连续10个月,每个月从该小区居民中随机抽取1户,若取到的是第一类居民,则发放礼品一份,设



正确答案
(1)中位数:155,平均数:156.8
(2)
(3)E(X)=8,D(X)=1.6
解析
(1)因为在频率分布直方图上,中位数的两边面积相等,可得中位数为155. (2分)
平均数为
(2)由频率分布直方图可知,采用分层抽样抽取10户居民,其中8户为第一类用户,2户为第二类用户,则从该10户居民中抽取2户居民且这两户居民用电资费不属于同一类型的概率为
(3)由题可知,该小区内第一类用电户占80%,则每月从该小区内随机抽取1户居民,是第一类居民的概率为0.8,则连续10个月抽取,获奖人数


知识点
学校组织了一场科普知识大赛,共分两组,其中甲组优胜者有2名女生和m
(1)若选出的4名同学中恰有1名女生的概率是
(2)当m=2时,设选出的4名同学中女生人数为x,男生人数为y,记

正确答案
见解析。
解析
(1)设“从甲组内选出的2个同学均为男同学;从乙组内选出的同学中,1男1女”为事件



∴选出的4个同学中恰有1个女生的概率为

(2)
∴
∴
知识点
某产品按行业生产标准分成







(1)从该厂生产的产品中随机抽取
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数


(2)已知该厂生产一件该产品的利润y(单位:元)与产品的等级系数



正确答案
见解析
解析
解析:(1)由样本数据知,30件产品中等级系数
∴样本中一等品的频率为

二等品的频率为

三等品的频率为

(2)∵
用样本的频率分布估计总体分布,将频率视为概率,由(1)可得


∴可得
其数学期望
知识点
为调查某校学生喜欢数学课的人数比例,采用如下调查方法:
(1)在该校中随机抽取100名学生,并编号为1,2,3, ,100;
(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;
(3)请下列两类学生举手:(ⅰ)摸到白球且号数为偶数的学生;(ⅱ)摸到红球且不喜欢数学课的学生.
如果总共有26名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是( )
正确答案
解析
设该校学生中喜欢数学课的人数比例大约是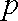

知识点
扫码查看完整答案与解析


































