- 概率与统计
- 共1631题
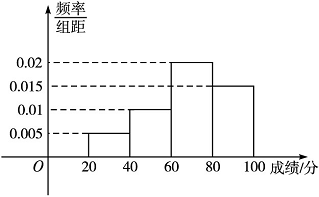
3.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是

正确答案
知识点
某险种的基本保费为
设该险种一续保人一年内出险次数与相应概率如下:
19.求一续保人本年度的保费高于基本保费的概率;
20.若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
21.求续保人本年度的平均保费与基本保费的比值.
正确答案
(Ⅰ)0.55;
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
试题解析:(Ⅰ)设

考查方向
解题思路
(Ⅰ)根据互斥事件的概率公式求一续保人本年度的保费高于基本保费的概率;
易错点
相关知识点不熟容易出错。
正确答案
(Ⅱ)
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
(Ⅱ)设


又
因此所求概率为
考查方向
解题思路
(Ⅱ)一续保人本年度的保费高于基本保费,当且仅当一年内出险次数大于3,由条件概率公式求解;
易错点
相关知识点不熟容易出错。
正确答案
(Ⅲ)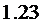
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
⑶解:设本年度所交保费为随机变量
平均保费

∴平均保费与基本保费比值为
考查方向
解题思路
(Ⅲ)记续保人本年度的保费为

易错点
相关知识点不熟容易出错。
2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:


19.求
20.按消防安全等级利用分层抽样的方法从这
正确答案
详见解析
解析
(Ⅰ)由已知可得;0.30+2m+m+0.10=1,解得:m=0.20. ……………………2分
所以
考查方向
概率和统计的计算
解题思路
按照统计的相关数据计算
易错点
数据不敏感,计算错误
正确答案
详见解析
解析
(Ⅱ)由(Ⅰ)知,利用分层抽样的方法从中抽取10家公司,则消防安全等级为一级的有3家,二级的有4家,三级的有2家,四级的有1家. ……………………6分
记消防安全等级为二级的4家公司分别为A,B,C,D,三级的2家公司分别记为











记“抽取的2家公司的消防安全等级都是二级”为事件M,则事件M包含的结果有:(A,B)(A,C)(A,D)(B,C)(B,D)(C,D)…共6种,……………………10分
所以
考查方向
分层抽样,随机事件发生的概率
解题思路
分情况讨论所可能发生的情况,然后计算概率
易错点
先求出所有出现的可能,然后算题目要求的可能,求二者的比例
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在样本的频率分布直方图中,一共有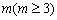

正确答案
解析
略。
知识点
某班

(1)求图中
(2) 从成绩不低于






正确答案
(1)
(2) 

解析
(1)由
解得
(2)成绩不低于

成绩在


随机变量




所以


知识点
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15,则该班的学生人数是( )。
正确答案
解析
由频率分布直方图,低于60分的同学所占频率为(0.005+0.01)×20=0.3,故该班的学生人数为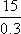
知识点
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元,根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示,经销商为下一个销售季度购进了130 t该农产品,以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润。
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望。
正确答案
(1) 
解析
(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000,
当X∈[130,150]时,T=500×130=65 000.
所以
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
(3)依题意可得T的分布列为
所以ET=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59 400
知识点
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取
本,称出它们的重量(单位:克),重量分组区间为



由此得到样本的重量频率分布直方图,如图
(1)求
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第



则样本数据的平均值为
(3)从盒子中随机抽取



正确答案
见解析。
解析
(1) 解:由题意,得
解得
(2)解:

由样本估计总体,可估计盒子中小球重量的平均值约为
(3)解:利用样本估计总体,该盒子中小球重量在








∴
∴
(或者
知识点
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图),已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间
(1)求直方图中

(2)从甲、乙两个班每天平均学习时间大于




正确答案
见解析
解析
(1)由直方图知,

因为甲班学习时间在区间

所以甲班的学生人数为

所以甲班学习时间在区间

(2)乙班学习时间在区间

由(1)知甲班学习时间在区间

在两班中学习时间大于







所以随机变量

知识点
某中学从某次考试成绩中抽取若干名学生的分数,并绘制
成如图1的频率分布直方图,样本数据分组为




样的方法从样本中抽取分数在
则其中分数在
正确答案
解析
略
知识点
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天
若网购金额超过

义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
(1)试确定



(2)该营销部门为了进一步了解这
达人”中用分层抽样的方法确定





正确答案
见解析。
解析
(1)根据题意,有
解得


补全频率分布直方图如图所示。
(2)用分层抽样的方法,从中选取
其中“网购达人”有

故




所


知识点
某市规定,高中学生三年在校期间参加不少于






(1)求抽取的


(2)从全市高中学生(人数很多)中任意选取





正确答案
见解析
解析
(1)根据题意,
参加社区服务时间在时间段

参加社区服务时间在时间段

所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为
所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的
概率估计为
(2)由(1)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为
由已知得,随机变量

所以



随机变量
因为 


知识点
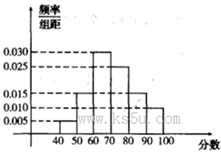
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为_________。
正确答案
400
解析
略
知识点
扫码查看完整答案与解析