- 概率与统计
- 共1631题
在长为12cm的线段AB上任取一点C.现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为
正确答案
解析
根据程序框图可计算得

因此输出的值与
知识点
某电视台组织一档公益娱乐节目,规则如下:箱中装有2个红球3个白球,参与者从中随机摸出一球,若为白球,将其放回箱中,并再次随机摸球;若为红球,则红球不放回并往箱中添加一白球,再次随机摸球,如果连续两次摸得白球,则摸球停止,设摸球结束时参与者摸出的红球数是随机变量誉,受益人获得的公益金y,与摸出的红球数ξ的关系是y=20000+5000ξ(单位:元)。
(1)求在第一次摸得红球的条件下,赢得公益金为30000元的概率;
(2)求随机变量ξ的分布列与期望。
正确答案
见解析。
解析
(1)在摸得第一个红球的条件下,箱内有1个红球4个白球,
摸球结束时羸得公益金为30000元的情形是:
先摸得红球或先摸得白球再摸得红球,其概率为:
p=

(2)随机变量ξ的可能取值为0,1,2,
对应的随机变量yξ的取值为20000,25000,30000,
∵P(ξ=0)=(

P(ξ=1)=(


P(ξ=2)=1﹣

∴随机变量yξ的分布列为:
∴Eyξ=20000×


知识点
体育测试成绩分为四个等级:优、良、中、不及格,某班50名学生参加测试的结果如下:
(1)从该班任意抽取1名学生,求这名学生的测试成绩为“良”或“中”的概率;
(2)测试成绩为“优”的3名男生记为




任选2人参加学校的某项体育比赛。
① 写出所有等可能的基本事件;
② 求参赛学生中恰有1名女生的概率。
正确答案
见解析
解析
(1)记“测试成绩为良或中”为事件

为事件


由已知,有
因为当事件


所以由互斥事件的概率公式,得

(2)① 有10个基本事件:









② 记“参赛学生中恰好有1名女生”为事件
事件






故所求的概率为
答:(1)这名学生的测试成绩为“良”或“中”的概率为
(2)参赛学生中恰有1名女生的概率为
知识点
某市质监部门对市场上奶粉进行质量抽检,现将9个进口品牌奶粉的样品编号为1,2,3,4,…,9;6个国产品牌奶粉的样品编号为10,11,12,…,15,按进口品牌及国产品牌分层进行分层抽样,从其中抽取5个样品进行首轮检验,用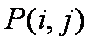
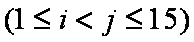
(1)求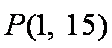
(2)求所有的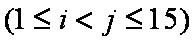
正确答案
见解析。
解析
(1)由分层抽样可知:首轮检验从编号为1,2,3,…,9的洋品牌奶粉的样品中抽取3个,从编号为10,11,…,15的国产品牌奶粉的样品中抽取2个,故
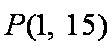
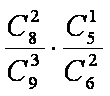
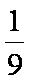
(2)①当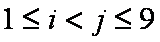
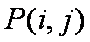
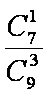
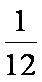
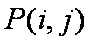
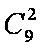
②当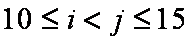
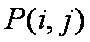
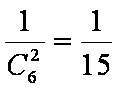
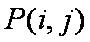
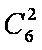
③当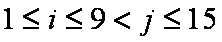
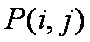
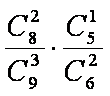
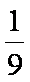
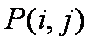
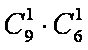
所以,所有的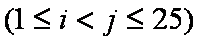
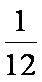
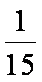
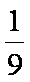
知识点
某学校为了增强学生对消防安全知识的了解,举行了一次消防安全知识竞赛,其中 一道题是连线题,要求将4种不同的工具与它们的4种不同的用途一对一连线,规定:每连对一条得5分,连错一条得-2分。某参赛者随机用4条线把消防工具与用 途一对一全部连接起来。
(1)求该参赛者恰好连对一条的概率。
(2)设X为该参赛者此题的得分,求X的分布列与数学期望。
正确答案
(1)
解析
(1)
(2) 









且
知识点
合肥市环保总站发布2014年1月11日到1月20日的空气质量指数(AQI),数据如下:153、203、268、166、157、164、268、407、335、119,则这组数据的中位数是 。
正确答案
184.5
解析
把这组数据按照从小到大的顺序排列,
119,153,157,164,166,203,268,268,335,407;
∴这组数据的中位数是
故答案为:184.5
知识点
某校举行中学生“珍爱地球·保护家园”的环保知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题

(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为,试求的分布列和数学期望。
正确答案
见解析
解析
(1)设“选手甲进入复赛”为事件,则选手甲答了3题都对进入复赛概率为:
或选手甲答了4个题,前3个2对1错,第4次对进入复赛

选手甲进入复赛的概率
(2)的可能取值为3,4,5,对应的每个取值,选手甲被淘汰或进入复赛的概率

的分布列为:

知识点
某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
统计结果显示:100位顾客中购物款不低于100元的顾客占60%。据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件).(注:视频率为概率)
(1)试确定m,n的值,并估计该商场每日应准备纪念品的数量;
(2)现有4人去该商场购物,求获得纪念品的人数ξ的分布列与数学期望.
正确答案
见解析
解析
解析:(1)由已知,100位顾客中购物款不低于100元的顾客有


该商场每日应准备纪念品的数量大约为 
(2)由(1)可知1人购物获得纪念品的频率即为概率

故4人购物获得纪念品的人数



……………………11分

或由
知识点
某地区注重生态环境建设,每年用于改造生态环境总费用为x亿元,其中用于风景区改造为y亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少a亿元,至多b亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%。若a=1,b=4,请你分析能否采用函数模型y=
正确答案
见解析
解析
解析:∵
∴函数y=
设
则
令

当



当



又





∴当

当




∴ 能采用函数模型y=
知识点
江西省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身 高服从正态分布N(170.5,16)。现从我校高三年 级男生中随机抽取50名测量身高,测量发现被 测学生身高全部介于157. 5cm和187.5 cm之 间,
(1)试评估我校高三年级男生在全省高中男生中的平均身高状况;
(2)求这50名男生身高在177.5cm以上(含177.5 cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人中身高排名(以高到低)在全省前130名的人数记为

参考数据:
若
正确答案
见解析
解析
(1)由直方图,经过计算我校高三年级男生平均身高为

(2)由频率分布直方图知,后两组频率为0.2,人数为0.2×50=10,即这50名男生身高在177.5cm以上(含177.5 cm)的人数为10人.
(3)

所以,全省前130名的身高在182.5 cm以上,这50人中182.5 cm以上的有5人.
随机变量




知识点
给出下列5种说法:
①在频率分布直方图中,众数左边和右边的直方图的面积相等;②标准差越小,样本数据的波动也越小;③回归分析就是研究两个相关事件的独立性;④在回归分析中,预报变量是由解释变量和随机误差共同确定的;⑤相关指数

其中说法正确的是
正确答案
②④⑤
解析
由统计学的相关定义可知,②④⑤的说法正确.
知识点
今年来,随着地方经济的发展,劳务输出大省四川、河南、湖北、安徽等地的部分劳务人员选择了回乡就业,因而使得沿海地区出现了一定程度的用工荒.今年春节过后,沿海某公司对来自上述四省的务工人员进行了统计(见下表):
为了更进一步了解员工的来源情况,该公司采用分层抽样的分法从上述四省工人员工中随机抽50名参加问卷调查。
(1)从参加问卷调查的50名务工人员中随机抽取两名,求这两名来自同一个省份的概率;
(2)在参加问卷调查的50名务工人员中,从来自四川、湖北两省的人员中随机抽取两名,用ξ表示抽得四川省务工人员的人数,求ξ的分布列和数学期望。
正确答案
见解析
解析
解析:(1)易得问卷调查中,从上述四省抽取的人数分别为
设“从参加问卷调查的

从参加问卷调查的

这两名人员来自同一省份的取法共有C



∴
(2)由(1)知,在参加问卷调查的






…………… 10分
∴

知识点
人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高,为了解某地区居民的幸福感情况,随机对该地区的男、女居民各500人进行了调查,调查数据如表所示:
根据表格,解答下面的问题:
(1)在下图中绘出频率分布直方图,并估算该地区居民幸福感指数的平均值;
(2)如果居民幸福感指数不小于6,则认为其幸福。为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取4对夫妻进行调查,用X表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求X的分布列及期望(以样本的频率作为总体的概率)。
正确答案
见解析
解析
(1)频率分布直方图如下...........3分
所求的平均值为0.01×2×1+0.015×2×3+ 0.2×2×5+0.15×2×7+0.125×2×9=6.46 ...................5分
(2)男居民幸福的概率为
女居民幸福的概率为
故一对夫妻都幸福的概率为0.5×0.6=0.3...........7分
因此X的可能取值为0,1,2,3,4,且X~B(4,0.3)
于是
X的分布列为
………………………………11分

知识点
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000 株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
(1) 现采用分层抽样的方法,从这个样本中取出10株玉米,再从这10株玉米中随机 选出3株,求选到的3株之中既有圆粒玉米又有皱粒玉米的概率;
(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下 认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:


正确答案
(1)
解析
(1) 现采用分层抽样的方法,从样本中取出的10株玉米中圆粒的有6株,皱粒的有4株,所以从中再次选出3株时,既有圆粒又有皱粒的概率为
(2) 根据已知列联表:
所以
又
知识点
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组




(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好” 的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有

正确答案
见解析。
解析
(1)其它组的频率为(0.01+0.07+0.06+0.02)×5=0.8,所以第四组的频率为0.2,频率分布图如图:

(2)依题意优秀与良好的人数比为3:2,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,记从这5人中选2人至少有1人是优秀为事件



(3)由频率分布直方图可知,第四组的人数为8人,第五组的人数为4人,






知识点
扫码查看完整答案与解析