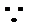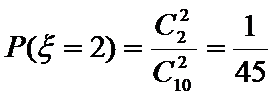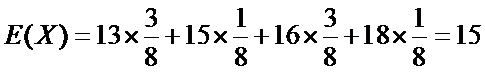- 概率与统计
- 共1631题
3．下图是2009年全国少数民族运动会上，七位评委为某民族舞蹈打出的分数的茎叶统计图，去掉一个最低分和一个最高分后，所剩数据的平均数和方差分别为（ ）．
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：
（1）如果y对x有线性相关关系，求回归直线方程；
（2）若实际生产中，允许每小时的产品中有缺点的零件最多为89个，那么机器的运转速度应控制在什么范围内？（参考数值：
正确答案
（1）
∴ 
∴ 回归直线方程为：
（2） 
解析
解析已在路上飞奔，马上就到！
知识点
17．前不久，省社科院发布了2013年度“城市居民幸福排行榜”，某市成为本年度城市最“幸福城市”．随后，树德中学校学生会组织部分同学，用“10分制”随机调查“新华西路”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎，小数点后的一位数字为叶)：
（1）指出这组数据的众数和中位数；
（2）若幸福度不低于9．5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
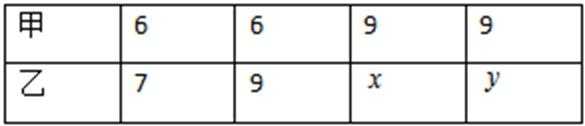
6．以下茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩（单位：分）。已知甲组数据的众数为124，乙组数据的平均数即为甲组数据的中位数，则
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
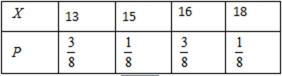
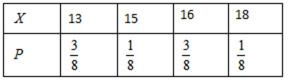
17．近几年来，我国许多地区经常出现干旱现象，为抗旱经常要进行人工降雨。现由天气预报得知，某地在未来5天的指定时间的降雨概率是：前3天均为50%，后2天均为80%，5天内任何一天的该指定时间没有降雨，则在当天实行人工降雨，否则，当天不实施人工降雨。
（1）求至少有1天需要人工降雨的概率；
（2）求不需要人工降雨的天数x的分布列和期望。
正确答案
（1）5天全不需要人工降雨的概率是
故至少有1天需要人工降雨的概率是
（2）x的取值是0,1,2,3,4,5，由（1）知
4天不需要人工降雨的概率是：
2天不需要人工降雨的概率是：
1天不需要人工降雨的概率是：
0天不需要人工降雨的概率是：
不需要人工降雨的天数x分布列是
不需要人工降雨的天数x的期望是：
解析
解析已在路上飞奔，马上就到！
知识点
5.已知一组数据a,b,9,10,11的平均数为10,方差为2,则
正确答案
解析
由题意可得a+b=20,(a-10)2+(b-10)2=8,
解得a=8,b=12或a=12,b=8.故
知识点
14.从0,1,2,3,…,9这10个数中任取5个不同的数,则这5个数的中位数是5的概率等于_______.
正确答案
解析
从0,1,2,3,…,9这10个数中任取5个不同的数,共有
知识点
4.某地气象局把2015年11月的每一天的最低气温作了统计,并绘制了如图所示的频率分布直方图,假设该月温度的中位数为me,众数为m0,平均数为
Ame=m0=
Bme=m0<
Cme<m0<
Dm0<me<
正确答案
解析
从表中看出,温度值的众数m0=5.由频率分布直方图,知30天最低温度值分布为3度(2天),4度(3天),5度(10天),6度(6天),7度(3天),8度(2天),9度(2天),10度(2天),则中位数me=
知识点
7.在一次演讲比赛中,七位评委为某参赛选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数与众数之和为________.
正确答案
169
解析
由题意可知,所剩数据的平均数为
知识点
18．某人5次上班途中所花的时间（单位：分钟）分别为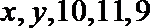
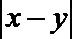
正确答案
解析
x+y+30=50,(x-10)2+(y-10)2+1+1=10,解得（x-y）2=16。B选项不正确，C选项不正确，D选项不正确，所以选A选项。
考查方向
本题主要考查统计
解题思路
1、表示出平均数和方差；
2、联立解方程，即可得到结果。
易错点
本题易在求方差时发生错误。
知识点
5.如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为（ ）
A
B
C
D
正确答案
解析
由题可知，甲的平均成绩为90，乙的平均成绩由污损部分确定，可供选择的数据为0到9十个，比甲的平均成绩小的有0到7 。A选项不正确，B选项不正确，D选项不正确，所以选C选项。
考查方向
解题思路
本题考查概率计算的问题，解题步骤如下：利用茎叶图求解即可
易错点
本题易在确定方法数时发生错误。
知识点
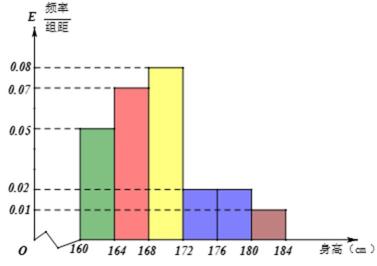
18．某市一次全市高中男生身高统计调查数据显示：全市100 000名男生的身高服从正态分布N(168，16).现从某学校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于160 cm和184 cm之间，将测量结果按如下方式分成6组：第一组 [160，164]，第二组[164，168]，…，第6组[180，184]，下图是按上述分组方法得到的频率分布直方图．
（Ⅰ）试评估该校高三年级男生在全市高中男生中的平均身高状况；
（Ⅱ）求这50名男生身高在172 cm以上（含172 cm）的人数；
（Ⅲ）在这50名男生身高在172 cm以上（含172 cm）的人中任意抽取2人，该2人中身高排名（从高到低）在全市前130名的人数记为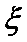
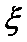
参考数据：若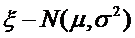
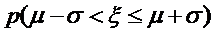
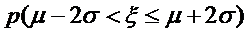
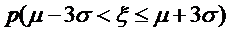
正确答案
（Ⅰ）平均值168.72,高于全市平均值
（Ⅱ）10人.
（Ⅲ）
解析
（Ⅰ）由直方图，经过计算该校高三年级男生平均身高为
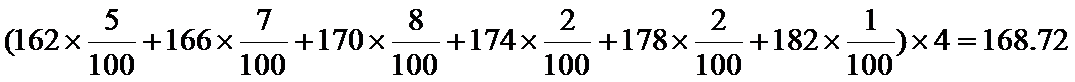
高于全市的平均值168（或者：经过计算该校高三年级男生平均身高为168.72，比较接近全市的平均值168）.
（Ⅱ）由频率分布直方图知，后三组频率为（0.02+0.02+0.01）×4＝0.2，人数为0.2×50＝10，即这50名男生身高在172 cm以上(含172 cm)的人数为10人.
（Ⅲ）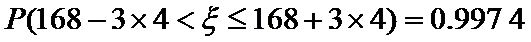
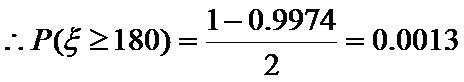
所以，全市前130名的身高在180 cm以上，这50人中180 cm以上的有2人.
随机变量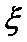
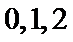
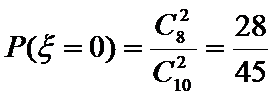
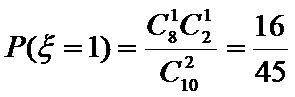
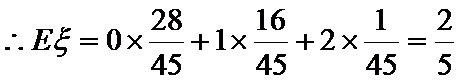
考查方向
解题思路
第一问估算，直接用每组的平均值乘以频率，然后相加即得
第二问先计算后三组的频率和，然后乘以总人数即得
第三问先根据正态分布概率计算出全市前130名是在那个身高区间，然后再计算50个人中有几个在这个区间，最后根据组合数计算出各变量的期望值，再相加即得。
易错点
1、对频率分布直方图认识不清，误把纵坐标当概率
2、对正态分布的意义理解不正确，不能正确计算概率
知识点
2.已知数据
A平均数增大，中位数
B平均数增大，中位数可能不变
C平均数可能不变，中位数可能不变
D
正确答案
解析
数据增加一个联系实际可知500超出体重，所以平均数会增加，50个数据的中位数可能为中间第25，26两个数（数值相等），所以增加一个最大数后，中位数变为第26个，不发生变化，所以选B
考查方向
解题思路
【解题思路】本题属于简单题，可使用直接法，
易错点
数据结合实际，忽视中位数的定义
知识点
6．气象意义上从春季进入夏季的标志为：“连续
①甲地：
②乙地：
③丙地：
则肯定进入夏季的地区有（ ）
正确答案
解析
由题可知，乙地、丙地的数据符合夏季的标志，甲地不符合。A选项不正确，B选项不正确，D选项不正确，所以选C选项。
考查方向
本题主要考查统计
解题思路
1、分析三地的温度情况；
2、按照条件判断，即可得到结果。
A选项不正确，B选项不正确，D选项不正确，所以选C选项。
易错点
本题易在判断语意时发生错误。
知识点
16．甲、乙两人进行射击比赛，各射击4局，每局射击10次，射击命中目标得1分，未命中目标得0分。 两人4局的得分情况如下：
（Ⅰ）若从甲的4局比赛中，随机选取2局，求这2局的得分恰好相等的概率；
（Ⅱ）如果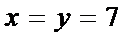
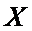
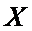
（Ⅲ）在4局比赛中，若甲、乙两人的平均得分相同，且乙的发挥更稳定，写出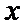
正确答案
（Ⅰ）
（Ⅱ）
（Ⅲ）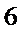
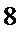
解析
试题分析：本题属于概率与统计的基本问题，题目的难点是逐渐由易到难，（1）直接按照步骤来求,(2)要注意正确求出每个变量对应的概率，（3）要注意利用离散型随机变量的分布列的性质验证分布列的正确性。
（Ⅰ）解：记 “从甲的4局比赛中，随机选取2局，且这2局的得分恰好相等”为事件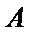
由题意，得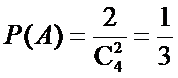
所以从甲的4局比赛中，随机选取2局，且这2局得分恰好相等的概率为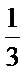
（Ⅱ）解：由题意，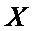
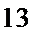
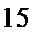
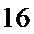
且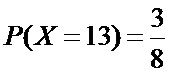
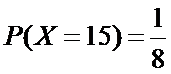
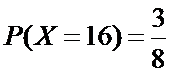
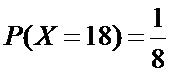
所以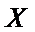
所以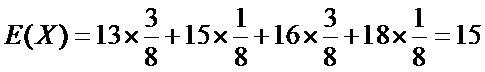
（Ⅲ）解：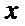
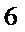
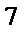
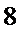
考查方向
本题主要考查了离散型随机变量的分布列、期望与方差，离散型随机变量的分布列大体有以下几类：
1．两点分布，
2．二项分布，超几何分布．
解题思路
本题考查离散型随机变量的分布列、期望与方差，解题步骤如下：
1．利用古典概型的概率公式进行求解；
2．写出随机变量的所有可能取值，分别求出每个变量对应的概率；
3．列表得到随机变量的分布列；
4．根据数学期望公式求其期望；
5．列出可能取值。
易错点
第二问中每个随机变量的概率不完全正确，导致结果错误。
知识点
扫码查看完整答案与解析