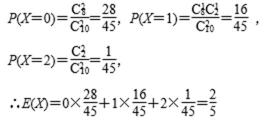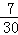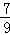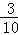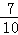- 概率与统计
- 共1631题
19.某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(1)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
正确答案
见解析。
解析
(1)芯片甲为合格品的概率约为
芯片乙为合格品的概率约为
(2)(ⅰ)随机变量X的所有取值为90,45,30,-15




所以,随机变量X的分布列为:
(ⅱ)设生产的5件芯片乙中合格品n件,则次品有5﹣n件.
依题意,得 50n﹣10(5﹣n)≥140,解得 
设“生产5件芯片乙所获得的利润不少于140元”为事件A,
则 
知识点
8.定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)的长度d=(2-1)+(5-3)=3.用[x]表示不超过x的最大整数,记{x}=x-[x],其中x∈R.设f(x)=[x]·{x},g(x)=x-1,当0≤x≤k时,不等式f(x)<g(x)的解集区间的长度为5,则k=( )
正确答案
解析
f(x)=[x]·{x}=[x]·(x-[x])=[x]x-[x]2,由f(x)<g(x),得[x]x-[x]2<x-1,即
知识点
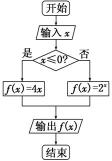
7.执行右图程序框图,如果输入的

正确答案
解析
若x=t=2,
则第一次循环,1≤2成立,则M= 
第二次循环,2≤2成立,则M= 
此时3≤2不成立,输出S=7,
故选:D.
知识点
18.某校从参加某次知识竞赛的同学中,选取






(1)求分数在
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率。
正确答案
(1)

解析
(1)分数在[70,80)内的频率为1﹣(0.010+0.015+0.015+0.025+0.005)×10=0.3,
∴小矩形的高为0.030,补全频率分布直方图如图:
(2)由频率频率分布直方图知前三组的频率之和为0.1+0.15+0.15=0.4,
∴中位数在第四组,设中位数为70+x,则0.4+0.030×x=0.5⇒x=
∴数据的中位数为70+

(3)第1组:
第6组:
共有36个基本事件,满足条件的有18个,所以概率为
知识点
17.工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别

(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为




(3)假定
正确答案
见解析。
解析
方法一:(1)无论以怎样的顺序派出人员,任务不能被完成的概率都是
(2)当依次派出的三个人各自完成任务的概率分别为

所需派出的人员数目的均值(数学期望)EX是
(3)(方法一)由(II)的结论知,当以甲最先、乙次之、丙最后的顺序派人时,
根据常理,优先派出完成任务概率大的人,可减少所需派出的人员数目的均值。
下面证明:对于


事实上,
即(*)成立。
方法二:(i)可将(2)中所求的EX改写为


(ii)也可将(2)中所求的EX改写为


序综合(i)(ii)可知,当
知识点
10.若从区间

正确答案
解析
略。
知识点
10.已知数列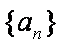
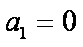
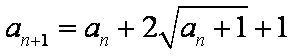
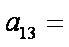
正确答案
解析
由an+1=an+2
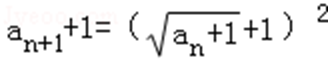
∴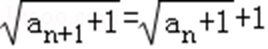
∴{
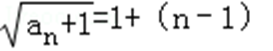
∴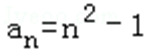
知识点
13.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有________。
正确答案
240种。
解析
根据题意,由排列可得,从6名志愿者中选出4人分别从事四项不同工作,有A=360种不同的情况,其中包含甲从事翻译工作,有A=60种,乙从事翻译工作,有A=60种,若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有360-60-60=240种。
知识点
17.某超市从2015年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个, 并按
假设甲、乙两种酸奶独立销售且日销售量相互独立
(1)写出频率分布直方图(甲)中


(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设

正确答案
见解析。
解析
(1)

(2)设事件
事件
事件
不高于20箱. 则

所以 
(3)由题意可知,




所以
所以 

另解:由题意可知
所以 

知识点
18.为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为

(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
正确答案
(1)平均数为36,众数为33
(2)E(X)=165.5元
(3)甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.
解析
(1)甲公司员工A投递快递件数的平均数为36,众数为33.
(2)设
当





(3)根据图中数据,可估算甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.
知识点
4.某市A,B,C,D四所中学报名参加某高校今年自主招生的学生人数如下表所示:
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查,则A,B,C,D四所中学,抽取学生数分别是多少名( )
正确答案
解析
由题意知,四所中学报名参加该高校今年自主招生的学生总人数为100,抽取的样本容量与总体个数的比值为=
知识点
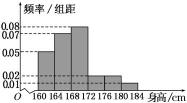
19.某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
(1)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(2)求这50名男生身高在172 cm以上(含172 cm)的人数;
(3)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前130名的人数记为X,求X的数学期望.
参考数据:
若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.682 6,
P(μ-2σ<X≤μ+2σ)=0.954 4,
P(μ-3σ<X≤μ+3σ)=0.997 4.
正确答案
见解析。
解析
(1)由频率分布直方图,经过计算得该校高三年级男生平均身高为
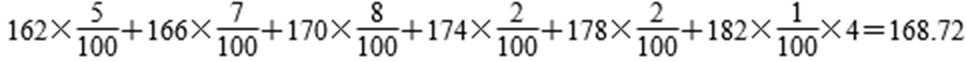
高于全市的平均值168.
(2)由频率分布直方图知,后3组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×50=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10.
(3)∵P(168-3×4<X≤168+3×4)=0.997 4,
∴P(X≥180)=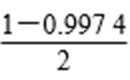
∴全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量X可取0,1,2,于是
知识点
2.根据给出的程序框图,计算f(-1)+f(2)=( )
正确答案
解析
输入-1,满足x≤0,所以f(-1)=4×(-1)=-4;
输入2,不满足x≤0,所以f(2)=22=4,
即f(-1)+f(2)=0.故选A.
知识点
5.任取实数a,b∈[-1,1],则a,b满足|a-2b|≤2的概率为( )
正确答案
解析
如图所示,则事件|a-2b|≤2所表示的区域为图中的阴影部分所表示的区域,易知直线a-2b=-2分别交直线a=-1与y轴于点
所以|BE|=
所以S△BEF=



易得△DHG≌△BEF.
因此S△DHG=S△BEF=
故阴影部分的面积
S=S四边形ABCD-2S△BEF=22-2×

由几何概型的概率公式可知,事件|a-2b|≤2的概率

知识点
6.10件产品中有3件次品,不放回地抽取2次,在第1次抽出的是次品的前提下,则第2次抽出正品的概率是( )
正确答案
解析
略。
知识点
扫码查看完整答案与解析