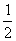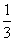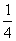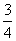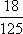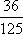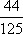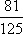- 概率与统计
- 共1631题
某公司有10万元资金用于投资,如果投资甲项目,根据市场分析知道:一年后可能获利10﹪,可能损失10﹪,可能不赔不赚,这三种情况发生的概率分别为



(1)如果把10万元投资甲项目,用


(2)若把10万元投资投资乙项目的平均收益不低于投资甲项目的平均收益,求
正确答案
见解析。
解析
(1)依题意,



(2)设

依题意要求
∴
知识点
春节期间,某商场决定从3种服装、2种家电、3种日用品中,选出3种商品进行促销活动。
⑴)试求选出的3种商品中至少有一种是家电的概率;
⑵商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高100元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为



正确答案
见解析。
解析
(1)设选出的3种商品中至少有一种是家电为事件A,从3种服装、2种家电、3种日用品中,选出3种商品,一共有
选出的3种商品中,没有家电的选法有
所以,选出的3种商品中至少有一种是家电的概率为
(2)设顾客三次抽奖所获得的奖金总额为随机变量
其所有可能的取值为0,



同理,
顾客在三次抽奖中所获得的奖金总额的期望值是
由
所以故m最高定为
知识点
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班.假设道路






(1)求李生小孩按时到校的概率;
(2)李生是否有七成把握能够按时上班?
(3)设

正确答案
见解析。
解析
(1)因为道路D、E上班时间往返出现拥堵的概率分别是

因此从甲到丙遇到拥堵的概率是
所以李生小孩能够按时到校的概率是
(2)甲到丙没有遇到拥堵的概率是
丙到甲没有遇到拥堵的概率也是
甲到乙遇到拥堵的概率是
甲到乙没有遇到拥堵的概率是

(3)依题意






分布列是:

知识点
方程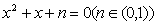
正确答案
解析
由一元二次方程有实根的条件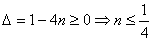
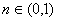
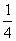
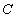
知识点
某产品经过4次革新后,成本由原来的120元下降到70元。若每次革新后,成本下降的百分率相同,那么,每次革新后成本下降的百分率为 (精确到0.1%)。
正确答案
12.6%
解析
略
知识点
盒子中装有形状、大小完全相同的3个红球和2个白球,从中随机取出一个记下颜色后放回,当红球取到2次时停止取球,那么取球次数恰为3次的概率是
正确答案
解析
略
知识点
如图,在棱长为2的正方体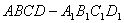
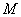
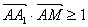
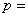
正确答案
解析
略
知识点
一支田径队有男运动员 56 人,女运动员 42 人,若用分层抽样的方法从全体运动员中抽出一个容量为 28 的样本,则样本中女运动员的人数为
正确答案
解析
略
知识点
一个箱中原来装有大小相同的 5个球,其中 3个红球,2个白球,规定:进行一次操作是指“从箱中随机取出一个球,如果取出的是红球,则把它放回箱中;如果取出的是白球,则该球不放回,并另补一个红球放到箱中。”
(1)求进行第二次操作后,箱中红球个数为4的概率;
(2)求进行第二次操作后,箱中红球个数的分布列和数学期望。
正确答案
见解析。
解析
知识点
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
现从第一小组、第二小组中各任选2人分析选课情况.
(1)求选出的4 人均选科目乙的概率;
(2) 设

正确答案
见解析。
解析
(1)设“从第一小组选出的2人选科目乙”为事件A,“从第二小组选出的2人选科目乙”为事件B,
由于事件A、B相互独立,且P(A)=

所以选出的4人均选科目乙的概率为:
P(A•B)=P(A)•P(B)=
(2)ξ可能的取值为0,1,2,3,
则P(ξ=0)=






ξ的分布列为:
所以ξ的数学期望为:0×



知识点
广东省汕头市日前提出,要提升市民素质和城市文明程度,促进经济发展有大的提速,努力实现“幸福汕头”的共建共享,现随机抽取50位市民,对他们的幸福指数进行统计分析,得到如下分布表:
(1)求这50位市民幸福指数的数学期望(即平均值);
(2)以这50人为样本的幸福指数来估计全市市民的总体幸福指数,若从全市市民(人数很多)任选3人,记ξ表示抽到幸福级别为“非常幸福或幸福”市民人数,求ξ的分布列;
(3)从这50位市民中,先随机选一个人,记他的幸福指数为m,然后再随机选另一个人,记他的幸福指数为n,求n<m+60的概率P。
正确答案
见解析。
解析
解:(1)记Ex表示这50位市民幸福指数的数学期望,
∴
(2)ξ的可能取值为0、1、2、3
∴ξ分布列为
(3)方法一:设所有满足条件的对立事件n≥m+60的概率为P1
①满足m=0且n=60的事件数为:
②满足m=0且n=90的事件数为:
③满足m=30且n=90的事件数为:
∴
所以满足条件n<m+60的事件的概率为
方法二:基本事件的总数为
满足条件n<m+60的有如下各种情况:
①满足m=0时,n=0,30的事件数为:
②满足m=30时,n=0,30,60的事件数为:
③满足m=60时,n=0,30,60,90的事件数为:
④满足m=90时,n=0,30,60,90的事件数为:
所以
知识点
容量为60的样本的频率分布直方图共有n(n>1)个小矩形,若其中一个小矩形的面积等于其余n﹣1个小矩形面积和的
正确答案
10
解析
∵分类分步直方图共有n个小矩形,
其中一个小矩形的面积等于其余(n﹣1)个小矩形面积之和的
设这一个小矩形的面积是x,则其余(n﹣1)个小矩形面积之和为5x,
∵x+5x=1,
∴x=
∵样本容量为60,
则这个小矩形对应的频数是60×
故答案为:10。
知识点
已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,x﹣y2≥0},若向区域Ω上随机投一点P,则点P落入区域A的概率是 。
正确答案
解析
∴ 作出Ω对应的平面区域,得到如图的Rt△OBC,其中B(6,0),C(0,6)
又∵A={(x,y)|x≤4,y≥0,x﹣y2≥0},
∴作出A对应的平面区域,得到曲线y=
且在x轴上方的平面区域,
其面积为S1=



∵Rt△OBC的面积为S=
∴向区域Ω上随机投一点P,则点P落入区域A的概率P=

故答案为:
知识点
我们把各位数字之和为6的四位数称为“六合数”(如2013是“六合数”),则“六合数”中首位为2的“六合数”共有( )
正确答案
解析
:设满足题意的“六合数”为
(1)一个为4,两个为0,共有3种;
(2)一个为3,一个为1,一个为0,共有A
(3)两个为2,一个为0,共有3种;
(4)一个为2,两个为1,共有3种。
则“六合数”中首位为2的“六合数”共有15种。
故选B。
知识点
有编号分别为1,2,3,4,5的5个红球和5个黑球,从中取出4个,则取出的编号互不相同的概率为( )
正确答案
解析
略
知识点
扫码查看完整答案与解析