- 概率与统计
- 共1631题
19.A、B是治疗同一种疾病的两种药,用若干试验进行对比试验,每个试验由4只小白鼠组成,其中2只服用A,另两只服用B,然后观察疗效,若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组,设每只小白鼠服用A有效的概率为

(1)求一个试验组为甲类组的概率;
(2)观察3个试验组,用

正确答案
解:(Ⅰ)设A1表示事件“一个试验组中,服用A有效的小白鼠有i只”,i= 0,1,2,
B1表示事件“一个试验组中,服用B有效的小白鼠有i只”,i= 0,1,2,依题意有
所求的概率为P = P(B0·A1)+ P(B0·A2)+ P(B1·A2=
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,
ξ的分布列为
数学期望
解析
解析已在路上飞奔,马上就到!
知识点
20.在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次:在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次。某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
(1)求随机变量ξ的数学期望E(ξ);
(2)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
正确答案
(2)用C表示事件“该同学选择第一次在A处投,以后都在B处投,得分超过3分”,
用D表示事件“该同学选择都在B处投,得分超过3分”,
则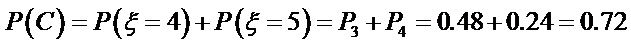
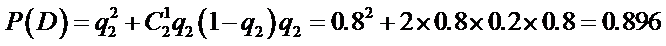
故P(D)>P(C).
即该同学选择都在B处投篮得分超过3分的概率大于该同学选择第一次在A处投以后都在B处投得分超过3分的概率。
解析
解析已在路上飞奔,马上就到!
知识点
10.电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成,则一天中任一时刻的四个数字之和为22的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地摸出4个球,求取出的红球数不小于黑球数的概率
(Ⅱ)若无放回地摸出4个球,
①求取出的红球数ξ的概率分布列和数学期望;
②求取出的红球数不小于黑球数的概率

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.一袋内装有大小相同的红色球6个,黄色球5个,蓝色球4个,同色球外部特征完全相同,从中任取4个球,则每种颜色的球至少取到1个的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙、丙三名射击运动员射中目标的概率分别为

(1)求
(2)在概率


正确答案
解:(1)设




所以


(2)由


可得


即实数

解析
解析已在路上飞奔,马上就到!
知识点
18.在一次数学考试中,第22题和第23题为选做题. 规定每位考生必须且只须在其中选做一题. 设某4名考生选做每一道题的概率

(1)求其中甲、乙两名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为

正确答案
解:(1)
(2)随机变量

∴
∴变量
解析
解析已在路上飞奔,马上就到!
知识点
18.某汽车驾驭学校在学员结业前对其驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核,若小张参加每次考核合格的概率依次组成一个公差为

(1)求小张第一次参加考核就会合格的概率
(2)求小张参加考核的次数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.为适应新课程改革的需要,调动学生学习的兴趣,拓宽学生学习的视野,某中学对高二年级理科、文科分别开设了三门选修课,学生是否选修哪门课互不影响。经对高二理科、文科各随机抽取50人进行问卷调查,获得数据如下:
若总体按此规律分布。
(1)求理科所选门数

(2)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙二人进行一次乒乓球比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为

(1)求甲获得这次比赛胜利的概率;
(2)设

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
11.每次抛掷一枚骰子(六个面上分别标以1,2,3,4,5,6)。连续抛掷2次,则2次向上的数之和不小于10的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某学校举行定点投篮考试,规定每人最多投篮4次,一旦某次投篮命中,便可得到满分,不再继续以后的投篮,否则一直投到第4次为止.如果李明同学参加这次测试,设他每次定点投篮命中的概率依次为0.6,0.7,0.8,0.9。
(1)求他在本次测试中投篮次数
(2)求他在本次测试中得到满分的概率。
正确答案
(1)随机变量
P(
P(

P(


P(


解析
解析已在路上飞奔,马上就到!
知识点
6.学校准备从5位报名同学中挑选3人,分别担任校运会中跳高、跳远和铅球3个不同项目比赛的志愿者.已知其中同学甲不能担任跳高比赛的志愿者,则不同的安排方法共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在的地区附近有A,B,C三家社区医院,并且他们对社区医院的选择是相互独立的.
(I)求甲、乙两人都选择A社区医院的概率;
(II)求甲、乙两人不选择同一家社区医院的概率;
(III)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
正确答案
解:(Ⅰ )设“甲、乙两人都选择A社区医院”为事件

所以甲、乙两人都选择A社区医院的概率为
(Ⅱ )设“甲、乙两人选择同一个社区医院”为事件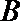
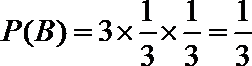
所以甲、乙两人不选择同一个社区医院的概率是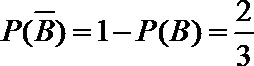
(Ⅲ )依题意
所以ξ的分布列为
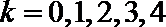
所以 
解析
解析已在路上飞奔,马上就到!
知识点
11.在二项式在二项式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析