- 概率与统计
- 共1631题
24.某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线。每连对一个得3分,连错得一1分,一名观众随意连线,他的得分记作X。
(1)求该观众得分非负的概率;
(2)求X的分布列及数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.源头学子餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种.现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需要不同的素菜品种( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.袋子A中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是
(Ⅰ)求恰好摸5次停止的概率;
(Ⅱ)记5次之内(含5次)摸到红球的次数为


正确答案
解
(Ⅰ)
(Ⅱ)随机变量
由n次独立重复试验概率公式

(或
随机变量


解析
解析已在路上飞奔,马上就到!
知识点
10.先后抛掷两枚质地均匀的骰子(各个面上分别标有


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
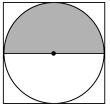
2.在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是( )
正确答案
解析
设正方形的边长为2,则豆子落在正方形内切圆的上半圆中的概率为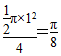
知识点
8.同时抛掷两个骰子,向上的点数之积为3的倍数的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.将容量为n的样本中的数据分成6组,绘制频率分布直方图. 若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n等于___________。
正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
18.2014年全国网球赛规定:比赛分四个阶段,只有上一阶段的胜者,才能继续参加下一阶段的比赛,否则就被淘汰,选手每闯过一个阶段,个人积10分,否则积0分.甲、乙两个网球选手参加了此次比赛.已知甲每个阶段取胜的概率为

(1)求甲、乙两人最后积分之和为20分的概率;
(2)设甲的最后积分为X,求X的分布列和数学期望.
.
正确答案
解:
(1)设“甲、乙两人最后积分之和为20分”为事件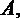
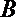

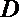
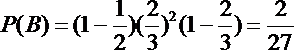

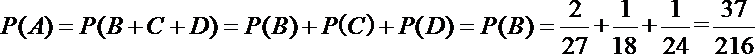
(2)X的取值可为: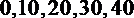
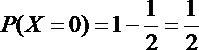
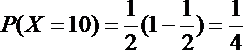
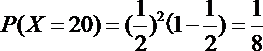
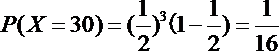
所以X的分布列可为
数学期望
解析
解析已在路上飞奔,马上就到!
知识点
17.中国
(1)根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数;
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用


正确答案
(1)根据志愿者的身高编茎叶图知湖北师范学院志愿者身高的中位数为:
(2)由茎叶图可知,“高个子”有8人,“非高个子”有12人,


“非高个子”为
则至少有1人为高个子的概率

(3)由题可知:湖北师范学院的高个子只有3人,
则
故



即






解析
解析已在路上飞奔,马上就到!
知识点
23.某商场为促销设计了一个抽奖模型,一定数额的消费可以获得一张抽奖券,每张抽奖券可以从一个装有大小相同的4个白球和2个红球的口袋中一次性摸出3个球,至少摸到一个红球则中奖。
(1)求一次抽奖中奖的概率;
(2)若每次中奖可获得10元的奖金,一位顾客获得两张抽奖券,求两次抽奖所得的奖金额之和X(元)的概率分布和期望E(X)。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.盒中装有5个乒乓球用作比赛,其中2个是旧球,另外3个是新球,新球使用后即成为了旧球。
(I)每次比赛从盒中随机抽取1个球使用,使用后放回盒中,求第2次比赛结束后盒内剩余的新球数为2个的概率
(II)每次比赛从盒中随机抽取2个球使用,使用后放回盒中,设第2次比赛结束后盒内剩余的新球数为X,求X的分布列和数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 在120°的二面角内放置一个小球,它与二面角的两个面相切于A、B两点,这两个点的距离AB=5, 则小球的半径为______________
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
18.某地区为下岗女职工免费提供财会和家政培训,以提高下岗女职工的再就业能力,每名下岗人员可以参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有50%,参加过家政培训的有80%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响。
(I)任选1名下岗女职工,求该人参加过培训的概率;
(II)任选3名下岗女职工,记


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.一只口袋装有形状、大小都相同的5只小球,其中2只白球,3只红球。从中一次随机摸出2只球,则2只球不同色的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一只口袋内装有大小相同的5只球,其中3只黑球,2只白球,从中一次随机摸出2只球,至少有1只黑球的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析