- 概率与统计
- 共1631题
16.设

正确答案
解析
由


考查方向
解题思路
先利用集合间的关系找出其对立事件,后即可得到答案。
易错点
1.不会将

知识点
13.将高三(1)班参加体检的36名学生,编号为:1,2,3,

正确答案
15
知识点
4.为防止部分学生考试时用搜题软件作弊,命题组指派5名教师对数学卷的选择题、填空题和解答题这3种题型进行改编,则每种题型至少指派一名教师的不同分派方法种数为( )
正确答案
解析
解:人数分配上有两种方式即1,2,2与1,1,3.
若是1,1,3,则有
若是1,2,2,则有
所以共有150种不同的方法,所以选A
考查方向
计数原理的应用
解题思路
根据题意,分析可得人数分配上有两种方式即1,2,2与1,1,3,分别计算两种情况下的情况数目,相加可得答案
易错点
考虑出现的情况时有重漏
知识点
13.总体编号为01,02,…19,20的20个个体组成.利用下面的随机数表选
取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为 .
正确答案
01
解析
从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读,
第一个数为65,不符合条件,第二个数为72,不符合条件,
第三个数为08,符合条件,
以下符合条件依次为:08,02,14,07,01,
故第5个数为01
考查方向
简单随机抽样,图表
解题思路
从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读,依次为65,72,08,02,63,14,07,02,43,69,97,28,01,98,…,其中08,02,14,07,01符合条件,故可得结论
易错点
对图表的性质掌握不好,概率统计感不强
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
① 每位参加者记分器的初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,记分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题A、B、C、D顺序作答,直至答题结束。
假设甲同学对问题A、B、C、D回答正确的概率依次为



(1)求甲同学能进入下一轮的概率;
(2)用ξ表示甲同学本轮答题结束时答题的个数,求ξ的分布列和数学期望Εξ。
正确答案
见解析。
解析
设A、B、C、D分别为第一、二、三、四个问题,用






所以 
(1)记“甲同学能进入下一轮”为事件
则 
由于每题答题结果相互独立,因此


(2)由题意,随机变量
由于每题答题结果相互独立,
所以,
因此 随机变量
所以
知识点
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示。
已知这100位顾客中的一次购物量超过8件的顾客占55%。
(1)确定

(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过
正确答案
(1)

(2)
解析
(1)由已知,得
该超市所有顾客一次购物的结算时间组成一个总体,所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本,将频率视为概率得

X的数学期望为

(2)记A为事件“该顾客结算前的等候时间不超过2.5分钟”,


由于顾客的结算相互独立,且

故该顾客结算前的等候时间不超过2.5分钟的概率为
知识点
两个实习生每人加工一个零件,加工为一等品的概率分别为

否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为
正确答案
解析
记两个零件中恰好有一个一等品的事件为A,则
P(A)=P(A1)+ P(A2)=
知识点
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
正确答案
见解析。
解析
(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
(2)设生产的4件甲产品中一等品有

由题设知

又


所求概率为
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
知识点
某车间共有

(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间
(3)从该车间


正确答案
见解析
解析
(1)由题意可知,样本均值
(2)

(3)

而恰有1名优秀工人有


知识点
给出下列命题:
(1)已知事件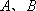
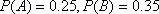
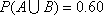
(2)已知事件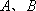
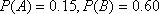
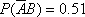
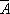
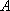
(3)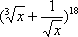
则其中真命题的序号是 [答]( )。
正确答案
解析
略
知识点
某个部件由三个元件如图4方式连接而成,元件A
或元件B正常工作,且元件C正常工作,则部件正
常工作,若3个元件的次品率均为
相互独立,那么该部件的次品率为 。
正确答案
解析
略
知识点
已知甲盒中仅有1个球且为红球,乙盒中有m个红球和n个篮球

(a)放入

(b)放入

则 ( )
正确答案
解析


∴


故
又∵
∴
又
∴
=



所以
知识点
某地为绿化环境,移栽了银杏树2棵,梧桐树3棵.它们移栽后的成活率分别为
(1)求银杏树都成活且梧桐树成活2棵的概率;
(2)求成活的棵树
正确答案
见解析。
解析
(1)设
设








(2)


同理:


∴
∴
知识点
扫码查看完整答案与解析





















































