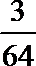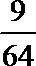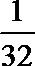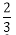- 概率与统计
- 共1631题
19.学校游园活动有这样一个游戏节目,甲箱子里装有3个白球、2个黑球;乙箱子里装有1个白球、2个黑球。这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在一次游戏中:①摸出3个白球的概率;②获奖的概率;
(Ⅱ)求在两次游戏中获奖次数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某单位从一所学校招收某类特殊人才.对
例如,表中运动协调能力良好且逻辑思维能力一般的学生有


(I) 求

(II)从参加测试的

(III)从参加测试的

生人数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.一个口袋中装有2个白球和


(1)试用含
(2)若
(3)记三次摸球恰有一次中奖的概率为


正确答案
解:(1)∵一次摸球从

任何一个球被选出都是等可能的,其中两球颜色相同有
∴一次摸球中奖的概率
(2)若

三次摸球是独立重复试验,三次摸球恰有一次中奖的概率是

(3)设一次摸球中奖的概率为
则三次摸球恰有一次中奖的概率为

∵
∴


∴当

∵


故当
解析
解析已在路上飞奔,马上就到!
知识点
17.合肥八中模拟联合国协会共有三个小组:中文组、英文组、辩论组,现有12名新同学(其中3名为男同学)被平均分配到三个小组.
(Ⅰ)求男同学甲被分到中文组,其他2名男同学被分到另外两个不同小组的概率;
(Ⅱ)若男同学所在的小组个数为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.箱中装有12张大小、质量一样的卡片,每张卡片正面分别标有1到12中的一个号码,正面号码为n的卡片反面标的数字是
(I)如果任意取出一张卡片,求正面数字不大于反面数字的概率;
(II)如果有放回地抽取三张卡片,用X表示三张中正面数字不大于反面数字的张数求X的分布列和数学期望。
(III)如果同时取出两张卡片,在正面数学无3的倍数的情况下,试求他们反面数字相同的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.一个质量均匀的正四面体型的模具,其四个面上分别标有数字1,2,3,4,若连续投掷三次,取三次面向上的数字分别作为三角形的边长,则其能构成钝角三角形的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.将一颗骰子投掷两次分别得到点数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.某品牌汽车的4S店,对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
(1)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位彩用分3期付款”的概率P(A);
(2)4S店销售一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.用


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某市今年1月份前30天空气质量指数(AQI)的趋势图如图:
当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月1日至10日中的某一天到达该市,并停留2天,若以空气质量优良的频率作为概率,则此人停留期间空气质量2天都是优良的概率为___________.
正确答案
解析
利用频率=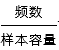
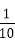
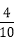

知识点
3.从集合{2,3,4,e,

正确答案
解析
从集合{2,3,4,e,

共有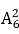
其中满足ab>1,共有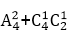
故ab>1的概率为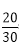
知识点
10.已知一个袋子里装有颜色不同的6个小球,其中白球2个,黑球4个,现从中随机取球,每次只取1个球.每次取球后都不放回袋中,取完所有白球就终止游戏,则取球4次游戏结束的概率为( ).
正确答案
解析
根据题意知,所求事件的概率为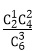
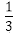
知识点
14.从0,1,2,3,…,9这10个数中任取5个不同的数,则这5个数的中位数是5的概率等于_______.
正确答案
解析
从0,1,2,3,…,9这10个数中任取5个不同的数,共有


知识点
4.袋中有大小相同的红球和白球各1个,每次任取1个,有放回地摸三次,三次摸到的球恰有两次颜色相同的概率( ).
正确答案
解析
(法一)摸到红球或白球的概率都是






(法二)所有基本事件为(红,红,红),(红,红,白),(白,红,红),(红,白,红),(白,红,白),(红,白,白),(白,白,红),(白,白,白),共8种.记“三次摸到的球恰有两次颜色相同”为事件A,则A所包含的基本事件为(红,红,白),(白,红,红),(红,白,红),(白,红,白),(红,白,白),(白,白,红),共6种,故P(A)=

知识点
12.两位老师批改同一篇作文,规定批改成绩都是正整数,假设两人批改的成绩都是两位正整数,且十位数字都是5,则两人批改的成绩之差的绝对值不超过2的概率为( ).
正确答案
解析
设甲的成绩为x,乙的成绩为y,且x,y∈{50,51,52,…,59},
则(x,y)对应如图所示的正方形ABCD内部的整数点,共有10×10=100,
其中满足
故所求概率为P=
知识点
16.甲、乙、丙、丁四人排成一排,其中甲、乙两人相邻的概率是
正确答案
解析
由A44=24,A22*A33=12,则P=
考查方向
本题主要考查排列组合、概率计算
解题思路
1、求出4人排队的总方法数;
2、求出甲乙相邻的方法数,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求方法数时发生错误。
知识点
扫码查看完整答案与解析