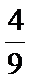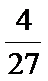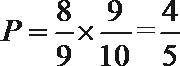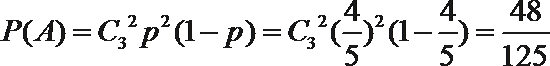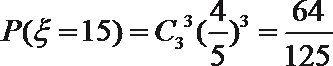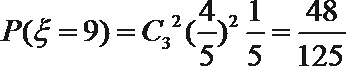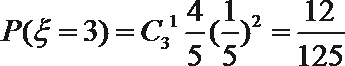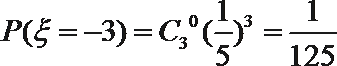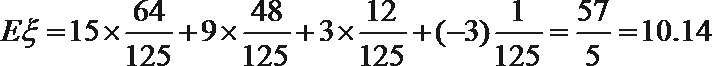- 概率与统计
- 共1631题
12.正四面体的四个面上分别写有数字0,1,2,3把两个这样的四面体抛在桌面上,则露在外面的6个数字之和恰好是9的概率为___________.
正确答案
解析
由题意,试验发生所包含的事件是2个均匀的正四面体与桌面接触,共有4×4=16种情况.一个正四面体的四个面的数字和为6,则露在外面的6个数字之和恰好是9即与桌面接触两个面的数字和为3,它包括0+3、1+2、2+1、3+0四种情况.∴所求概率为
考查方向
本题考查等可能事件的概率计算,是容易题,在近几年各地高考中频频出现.
解题思路
先求试验所包含的事件的所有种数,然后寻找符合要求的试验种数,即可得到概率.
易错点
解题的关键是正确运用列举法,分析得到基本事件的个数.
知识点
7.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球中有黄球的概率为___________
正确答案
解析
考查方向
解题思路
本题考查运用乘法原理求这2只球中没有黄球的概率,再利用互斥事件的性质求解。解题步骤如下:
易错点
本题必须注意审题,忽视则会出现错误。
知识点
3.从1,2,3,4这四个数中一次随机地取2个数,则所取2个数的乘积为偶数的概率是____________
正确答案
解析
随机地抽取2个数总可能数为6种,两个数之积为偶数的为:1,2;1,4;2,3;2,4;3,4,共有5种,那么所取的2个数之为偶数的概率为
考查方向
解题思路
本题考查了古典概型的求法,简单的运算推理能力。
解题步骤如下:写出基本事件的总数和满足条件的事件个数。根据古典概型的计算公式,求出结果。
易错点
本题易混淆古典概型与几何概型的意义,对基本事件的个数会遗漏。
知识点
9.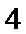

正确答案
解析
首先计算总数,4个人,每个人都可以在3项不同的活动中任选一项,也就是每个人都有3中选择,所以总数是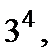
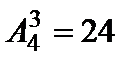
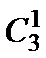
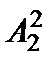
考查方向
解题思路
首先根据邮筒原理,算出总数,然后来计算每一项至少有一人参加共有多少种,最后计算概率
易错点
1、总数是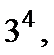
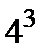
2、不会计算每项至少有一人参加的数量
知识点
18. 现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为

(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分

正确答案
见解析
解析
(Ⅰ)记“该射手恰好命中一次”为事件



由题意知,

由于
(Ⅱ)根据题意,

根据事件的独立性和互斥性得



故
所以
考查方向
解题思路
第一问将所有可能的情况列举出求解,第二问根据随机变量分布列的概念及特征,一次写出当随机变量取不同值得情况
易错点
列举情况不全面
知识点
6.从集合




正确答案
解析
记基本事件为
则事件“直线

因为所有的基本事件共有
所以所求概率
考查方向
解题思路
1.找出所有基本事件和满足条件的基本事件的个数;
2.利用概率公式计算,得出结果,应选C。
易错点
不能正确运用斜率和截距的几何意义找出满足条件的基本事件的个数,因而出现错误。
知识点
5.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股
正确答案
解析
从


其中只有
故这三个数构成一组勾股数的概率为
考查方向
解题思路
本题考查了古典概型的概率,算出基本事件总数,算出事件A发生的事件数,算出比值即可。
易错点
基本事件总数易算错。
知识点
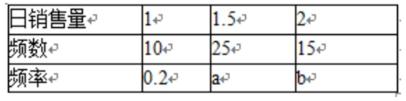
18.某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的结果如下:
(Ⅰ)求表中a,b的值
(Ⅱ)若以上表频率作为概率,且每天的销售量相互独立,
①求5天中该种商品恰有2天销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和(单位:千元),求X的分布列和期望.
正确答案
(Ⅰ)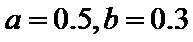
(Ⅱ)①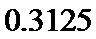
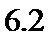
解析
(Ⅰ)∵
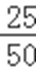
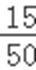
(Ⅱ)①依题意,随机选取一天,销售量为1.5吨的概率p=0.5
设5天中该种商品有X天的销售量为1.5吨,则X~B(5,0.5)
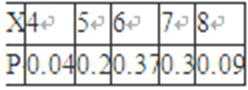
P(X=2)=C52×0.52×(1﹣0.5)3=0.3125 ②X的可能取值为4,5,6,7,8,则
p(X=4)=0.22=0.04 p(X=5)═2×0.2×0.5=0.2 p(X=6)═0.52+2×0.2×0.3=0.37
p(X=7)═2×0.3×0.5=0.3 p(X=8)=0.32=0.09
所有X的分布列为:
EX=4×0.04+5×0.2+6×0.37+7×0.3+8×0.09=6.2.
考查方向
解题思路
本题考查的是频率分布表,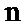

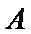
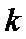
(Ⅰ)由于频率等于频数除以样本容量,所以可根据第二三组的频率求得a,b.
(Ⅱ)利用二项分布的概率公式求出5天中该种商品恰有2天的销售量为1.5吨的概率,求出X的可能取值为4,5,6,7,8,写出分布列,算出期望。
易错点
本题易在分析分布的时候出现错误,也可能在写离散型随机变量的时候出现错误。
知识点
16.在某班级举行的“元旦联欢会”有奖答题活动中,主持人准备了





(Ⅰ)记甲先回答问题



(Ⅱ)你觉得应先回答哪个问题才能使甲的得分期望更高?请说明理由.
正确答案
见解析
解析
(Ⅰ)



分布列为:

(Ⅱ)设先回答问题







分布列为:



考查方向
解题思路
根据所有可能情况列举出来求解,写出当随机变量取不同值时的情况。
易错点
求期望错误,分布列考虑问题不全
知识点
8.春节前,某市一过江大桥上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的6秒内任一时刻等可能发生,然后每串彩灯以6秒内间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过3秒的概率是( )
正确答案
解析
设两串彩灯分别在通电后x秒,y秒第一次闪亮,
则所有的可能情况对应的平面区域为正方形OABC,
作出直线x﹣y=3和直线y﹣x=3,则两灯在第一次闪亮时刻不超过3秒对应的平面区域为六边形ODEBGF,
∴P=


故选B.
考查方向
解题思路
1、由题意建立几何模型。
2、作出基本事件对应的平面区域和符合条件的平面区域,求出对应的概率。
易错点
本题易在由题意建立几何模型时出错。
知识点
8.学校有两个食堂,现有3名学生前往就餐,则三个人不在同一个食堂就餐的概率是____________.
正确答案
解析
由于学校有两个食堂,不妨令它们分别为食堂A、食堂B,三名学生选择每一个食堂的概率均为




考查方向
本题考查了互斥事件以及相互独立事件的概率,考查学生分析问题的能力.
解题思路
由于学校有两个食堂,不妨令它们分别为食堂A、食堂B,则三名学生选择每一个食堂的概率均为
易错点
混淆互斥事件与相互独立事件.
知识点
15.将一颗骰子投掷两次,第一次出现的点数记为








正确答案
解析
由题可知,P1=1/12,P2=8/9,代入圆的方程得m的取值范围是
考查方向
本题主要考查了概率及直线与圆的综合应用
解题思路
本题考查概率及直线与圆的综合应用,解题思路如下:
1、利用概率公式求出概率;
2、利用直线与圆的综合应用知识求解。
易错点
本题必须注意概率计算
知识点
19.生产甲乙两种元件,其质量按检测指标划分为:
指标大于或者等于


(1)试分别估计元件甲,乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利



在(1)的前提下:
①记

②求生产

正确答案
(1)
(2)66.
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
解:(1)元件甲为正品的概率约为:
元件乙为正品的概率约为:
(2)①随机变量




而且


所以随机变量
所以:
②设生产的


依题意,
解得:
所以

设“生产


则:
考查方向
本题考查了概率统计中的离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点
解题思路
本题考查概率统计,解题步骤如下:
1、利用已知求出甲、乙为正品的概率。
2、写出随机变量的取值,并求出相应的概率和数学期望
易错点
随机变量的取值及对应的概率。
知识点
17. 某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为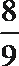
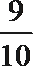
(I)求本月恰有两台仪器完全合格的概率;
(II)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为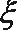
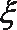
正确答案
解: (Ⅰ) 设恰有两台仪器完全合格的事件为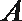
所以
(Ⅱ) 每月生产的仪器完全合格的台数可为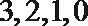
所以赢利额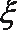
当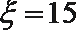
当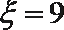
当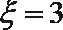
当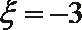
每月的盈利期望
所以每月的盈利期望值为
解析
见答案
考查方向
本题主要考查离散型随机变量的期望与方差,相互独立事件同时发生的概率,属于概率综合题,中档题。
解题思路
第1问直接用公式求解,第2问实际上求的是每月盈利的期望值。
易错点
计算能力弱
知识点
18.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,受到全国人民的瞩目。纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如下表所示:
(Ⅰ)若从抗战老兵中随机抽取2人进行座谈,求这2人参加纪念活动的环节数不同的概率;
(Ⅱ)某医疗部门决定从这些抗战老兵中(其中参加纪念活动的环节数为3的抗战老兵数大于等于3)随机抽取3名进行体检,设随机抽取的这3名抗战老兵中参加三个环节的有

正确答案
见解析
解析
试题分析:本题属于概率中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对应取值的概率.
(Ⅰ)设“这2名抗战老兵参加纪念活动的环节数不同”为事件

根据题意可知
由对立事件的概率计算公式可得
故这2名抗战老兵参加纪念活动的环节数不同的概率为
(Ⅱ)根据题意可知随机变量


则随机变量
则数学期望
考查方向
本题考查了离散型随机变量的概率分布列和数学期望,涉及到概率计算,是高考题中的高频考点.
解题思路
本题考查离散型随机变量的概率分布列和数学期望,解题步骤如下:
1、利用概率公式求解。
2、利用离散型随机变量的概率分布列和数学期望公式求解。
易错点
概率计算易错。
知识点
扫码查看完整答案与解析