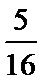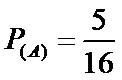- 概率与统计
- 共1631题
14.在

正确答案
知识点
4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为15oC,B点表示四月的平均最低气温约为5oC。下面叙述不正确的是
正确答案
知识点
12.小G和小M相约周末去欢乐谷游玩,他们约定周日早上8点至9点之间(假定他们在这一时间段内任一时刻等可能的到达)在欢乐谷正大门前集中前往,则他们中先到者等待的时间不超过15分钟的概率是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.圆






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在边长为1的正方形ABCD内任取一点P,则动点P到点A和C的距离都小于1的概率是( ).
正确答案
解析
满足条件的正方形ABCD如图所示,
其中满足条件的动点P的平面区域如图中阴影部分,
则正方形的面积S正方形=1,
阴影部分的面积S阴影=

故所求事件的概率为
知识点
9.不等式组

正确答案
解析
如图所示,作出不等组的可行域,根据几何概型的定义,可知红色区域面积与四边形ABCD的面积的比就是所求概率。红色区域面积不好求,由于是选择题,可以根据选项求得,容易得到,红色区域的面积比四边形面积的一半少,比四分之一多,所以结合选项,选择D
考查方向
解题思路
分别求出两个不等式组所表示的区域的面积,然后利用集合概型相关性质计算求得
易错点
区域求面积,不等式取值区间
知识点
12.由不等式组

正确答案
解析
做出区域A和B的位置,如下图,B为图中绿色部分,易得,A的面积为9,求B的面积应用积分,
考查方向
解题思路
根据题意做出图形,然后求出区域A和区域B的面积,进而求出概率
易错点
求不出区域B的面积
知识点
11. 已知曲线





正确答案
解析
由题可知:A的面积为
考查方向
解题思路
1、利用定积分表示A的面积;2、利用面积之比求解,即可得到结果。
易错点
本题易在表示面积时发生错误。
知识点
13.在长为10cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积不小于9cm2的概率为 .
正确答案
解析
设AC=x,则BC=10﹣x,
矩形的面积S=x(10﹣x)≥9,
∴x2﹣10x+9≤0,
∴1≤x≤9,
由几何概率的求解公式可得,矩形面积不小于9cm2的概率P= ,
故答案为: .
考查方向
解题思路
1、根据几何概型的概率公式,设AC=x,则BC=10﹣x,由矩形的面积S=x(10﹣x)≥9可求x的范围。
2、再利用几何概型的求解公式可求出概率。
易错点
本题易在由“矩形面积不小于9cm2”得到C所在范围时出错。
知识点
14.若不等式

正确答案
解析
由题可知SM=2π,SN=48,则P=
考查方向
本题主要考查线性规划及几何概型。
解题思路
解题步骤如下:1、画出平面区域。2、利用概率公式求解.
易错点
本题必须注意利用图像完成。
知识点
7.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 .
正确答案
知识点
从区间










正确答案
知识点
14.如图,
在平面直角坐标系







正确答案
解析
知识点
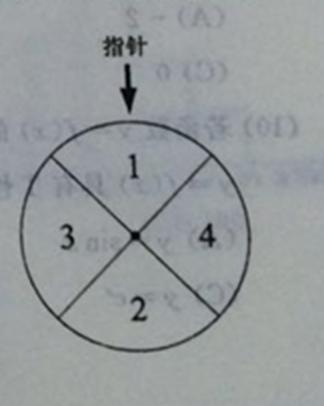
某儿童乐园在“六一”儿童节退出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若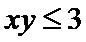
②若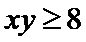
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
16.求小亮获得玩具的概率;
17.请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
正确答案
(1)
解析
(Ⅰ)设获得玩具记为事件A,获得水杯记为事件B,获得一瓶饮料记为事件C
转盘转动两次后获得的数据记为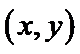
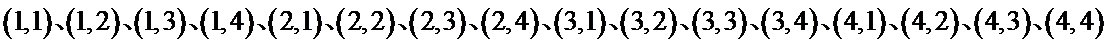
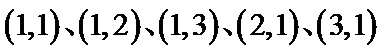
故小亮获得玩具的概率
考查方向
解题思路
事件A包含的基本事件共有五个,即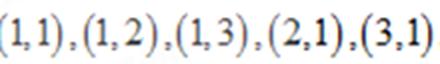
易错点
古典概型中基本事件空间的列举,对事件发生情况的分析,互斥事件概率的求解。
正确答案
(2)小亮获得水杯比获得饮料的概率大
解析
(Ⅱ)事件B为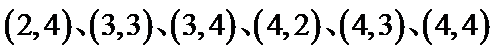
故小亮获得水杯的概率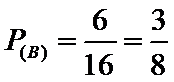
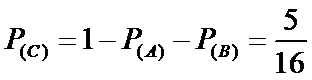
因为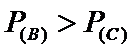
考查方向
解题思路
事件B包含的基本事件共有6个,事件C包含的基本事件共有5个,计算并比较即可;
易错点
古典概型中基本事件空间的列举,对事件发生情况的分析,互斥事件概率的求解。
20.(本题满分14分)
有一块正方形菜地


地分为两个区域





的分界线



点









纵坐标为



判断哪一个更接近于
正确答案
(1) 设分界线上任一点为
可得
(2) 设
∴
∴设所表述的矩形面积为
设五边形


∴五边形

知识点
扫码查看完整答案与解析