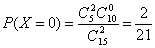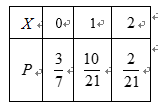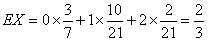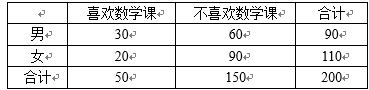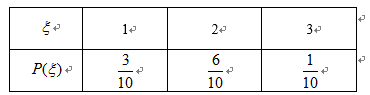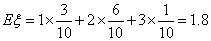- 概率与统计
- 共1631题
某工厂生产A,B两种元件,已知生产A元件的正品率为75%,生产B元件的正品率为80%,生产1个元件A,若是正品则盈利50元,若是次品则亏损10元;生产1个元件B,若是正品则盈利40元,若是次品则亏损5元。
(1)求生产5个元件A所得利润不少于140元的概率;
(2)设X为生产1个元件A和1个元件B所得总利润,求X的分布列和数学期望。
正确答案
见解析。
解析
知识点
今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
[来源:学。科。网]
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在


正确答案
见解析
解析
知识点
某单位从一所学校招收某类特殊人才,对
例如,表中运动协调能力良好且逻辑思维能力一般的学生有


(1)求

(2)从参加测试的

维能力优秀的学生的概率;
(3)从参加测试的

生人数为


正确答案
见解析
解析
(1)设事件

由题意可知,运动协调能力或逻辑思维能力优秀的学生共有
则
解得 
所以
(2)设事件


由题意可知,至少有一项能力测试优秀的学生共有
则
(3)





所以


所以
所以,
知识点
某个不透明的袋中装有除颜色外其它特征完全相同的8个乒乓球(其中3个是白色球,5个是黄色球),小李同学从袋中一个一个地摸乒乓球(每次摸出球后不放回),当摸到的球是黄球时停止摸球,用随机变量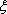

正确答案
解析
略
知识点
下表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良。
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度不超过75
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取3天,记


正确答案
见解析。
解析
(1)由上表数据知,10天中空气质量指数(AQI)小于100的日期有:
A2 、A3 、A5 、A9 、A10共5天,-
故可估计该市当月某日空气质量优良的概率
(2)由(1)知10天中表示空气质量为优良的天数为5,当天“PM2.5”的24小时平均浓度不超过75
故事件M发生的概率
(3)由(1)知,
且


故
-


知识点
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(1)从这15天的数据中任取3天的数据,记

(2)以这15天的PM2.5日均值来估计这360天的空气质量情况,则其中大约有多少天的空气质量达到一级.
正确答案
见解析。
解析
知识点
某地为绿化环境,移栽了银杏树2棵,梧桐树3棵.它们移栽后的成活率分别为
(1)求银杏树都成活且梧桐树成活2棵的概率;
(2)求成活的棵树
正确答案
见解析。
解析
(1)设
设








(2)


同理:


∴
∴
知识点
某市规定,高中学生三年在校期间参加不少于






(1)求抽取的


(2)从全市高中学生(人数很多)中任意选取





正确答案
见解析
解析
(1)根据题意,
参加社区服务时间在时间段

参加社区服务时间在时间段

所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为
所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的
概率估计为
(2)由(1)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为
由已知得,随机变量

所以



随机变量
因为 


知识点
为了调查我市在校中学生参加体育运动的情况, 从中随机抽取了16名男同学和14名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率, 从我市中学生中随机抽取3人,若其中喜爱运动的人数为

正确答案
见解析。
解析
(1)
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关
(3)统计结果中喜爱运动的中学生所占的频率为
喜爱运动的人数为


喜爱运动的人数为
因为


知识点
某公司为招聘新员工设计了一个面试方案:应聘者从






(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
正确答案
见解析
解析
(1)设甲正确完成面试的题数为





考生甲正确完成题数

设乙正确完成面试的题数为






考生乙正确完成题数

(2)因为

(或
所以
(或:因为

所以
综上所述,
从做对题数的数学期望考查,两人水平相当;
从做对题数的方差考查,甲较稳定;
从至少完成
知识点

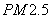
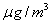
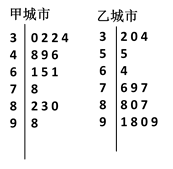
个值越高,就代表空气污染越严重:
甲、乙两城市2013年2月份中的15天对空气质量指数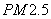
(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?
(注:不需说明理由)
(2)在乙城市15个监测数据中任取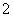
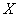
量类别为优或良的天数,求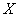
正确答案
见解析。
解析
(1)甲城市空气质量总体较好,
(2)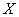
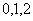
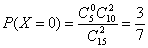
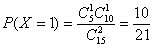
所以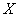
数学期望
知识点
正确答案
见解析
解析
(1)由题意可知



∴
(2)先用反证法证明
若
则
同理可知
由题目所有数和为
即
∴
与题目条件矛盾
∴
易知当

∴
(3)

首先构造满足



经计算知,



下面证明


由







设





考虑






故



知识点
李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有






(1)若走
(2)若走
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
正确答案
见解析
解析
知识点
为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下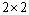
(1)根据独立性检验的基本思想,约有多大的把握认为“性别与喜欢数学课之间有关系”?
(2)若采用分层抽样的方法从不喜欢数学课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为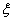
正确答案
见解析。
解析
(1)∵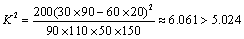
∴约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
(2)男生抽取的人数有: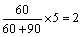
女生抽取的人数各有: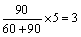
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,
所以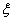
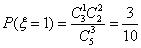
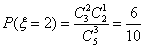
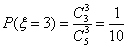
所以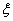
所以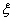
知识点
一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为

正确答案
解析
略
知识点
扫码查看完整答案与解析