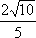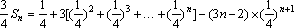- 运用诱导公式化简求值
- 共45题
11.已知:



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
一个几何体的三视图如图所示,其中主视图和左视图 是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为 ( )
正确答案
解析
略。
知识点
已知函数
(1) 当m=0时,求

(2) 当

正确答案
(1)
(2)m=-2
解析
(1)当m=0时,


从而得:
(2)
化简得:
当


代入上式,m=-2.
知识点
如图,在直角梯形









①当


②

③

其中所有正确结论的序号是_________.
正确答案
2,3
解析
略
知识点
一个空间几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
略
知识点
设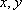
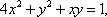
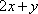
正确答案
解析
∵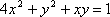
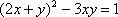
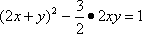
∴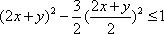
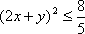
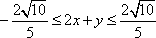
知识点
甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市。
由此可判断乙去过的城市为________。
正确答案
A
解析
由于甲没有去过B城市,乙没有去过C城市,但三人去过同一个城市,故三人去过的城市为A城市,又由于甲最多去过两个城市,且去过的城市比乙多,故乙只能去过一个城市,这个城市为A城市。
知识点
一个几何体的三视图如图所示(单位:m),则该几何体的体积为_________m3.
正确答案
解析
由三视图可该几何体为两个相切的球上方了一个长方体组成的组合体,所以其体积为:

知识点
在数列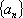
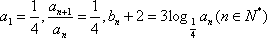
(1)求数列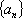
(2)求证:数列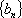
(3)设数列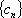

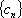
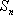
正确答案
见解析。
解析
(1)∵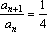
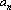


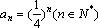
(2)∵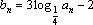
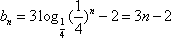
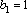
公差d=3,∴数列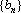
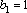
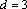
(3)由(1)、(2)知,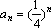

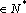
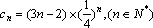
∴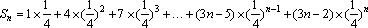
于是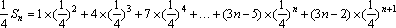
两式①-②相减得
=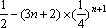
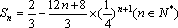
知识点
已知二次函数



(1)求a的值;
(2)

(3)若m=1,且x>0,求证:
正确答案
见解析。
解析
(1)解:∵关于


即不等式

∴
∴
∴
∴
(2)解法1:由(1)得
∴

∴
方程

①当

则



∴函数


∴函数

②当



若
故

∴函数

∴函数
若
则





∴函数



∴函数


综上所述, 当



当




(其中

解法2:由(1)得
∴

∴
若函数


令
得
则
方程(*)的两个实根为

设
①若



则



∴函数


∴函数

②若

又由(**)解得

故
则





∴函数



∴函数


综上所述, 当



当




(其中

(2)证法1:∵

∴

令
则

∵
∴

∴

证法2:下面用数学归纳法证明不等式
① 当


② 假设当


则

也就是说,当
由①②可得,对


知识点
扫码查看完整答案与解析