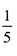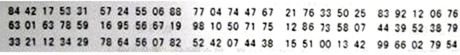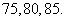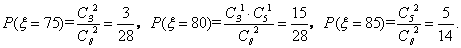- 古典概型与几何概型
- 共235题
某购物网站在2013年11月开展“全场6折”促销活动,在11日当天购物还可以再享受“每张订单金额(6折后)满300元时可减免100元”.某人在11日当天欲购入原价48元(单价)的商品共42件,为使花钱总数最少,他最少需要下的订单张数为()
正确答案
解析
略
知识点
某单位从一所学校招收某类特殊人才,对
例如,表中运动协调能力良好且逻辑思维能力一般的学生有


(1)求

(2)从参加测试的

维能力优秀的学生的概率;
(3)从参加测试的

生人数为


正确答案
见解析
解析
(1)设事件

由题意可知,运动协调能力或逻辑思维能力优秀的学生共有
则
解得 
所以
(2)设事件


由题意可知,至少有一项能力测试优秀的学生共有
则
(3)





所以


所以
所以,
知识点
有6人入住宾馆中的6个房间,其中的房号301与302对门,303与304对门,305与306对门,若每人随机地拿了这6个房间中一把钥匙,则其中的甲、乙两人恰好对门的概率为
正确答案
解析
略
知识点
袋中装有大小和形状相同的小球若干个黑球和白球,且黑球和白球的个数比为4:3,从中任取2个球都是白球的概率为

(1)求袋中原有白球、黑球的个数;
(2)求随机变量
正确答案
见解析。
解析
(1)依题意设袋中原有

由题意知
即

即袋中原有3个白球和4个黑球.
(2)依题意,



同理可得,

知识点
下表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良。
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度不超过75
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取3天,记


正确答案
见解析。
解析
(1)由上表数据知,10天中空气质量指数(AQI)小于100的日期有:
A2 、A3 、A5 、A9 、A10共5天,-
故可估计该市当月某日空气质量优良的概率
(2)由(1)知10天中表示空气质量为优良的天数为5,当天“PM2.5”的24小时平均浓度不超过75
故事件M发生的概率
(3)由(1)知,
且


故
-


知识点
某市规定,高中学生三年在校期间参加不少于






(1)求抽取的


(2)从全市高中学生(人数很多)中任意选取





正确答案
见解析
解析
(1)根据题意,
参加社区服务时间在时间段

参加社区服务时间在时间段

所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为
所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的
概率估计为
(2)由(1)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为
由已知得,随机变量

所以



随机变量
因为 


知识点
已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩拉样统计,先将800人按001,002,…,800进行编号。
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;
(下面摘取了第7行至第9行)
(2)抽取取100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求a,b的值。
(3)在地理成绩为及格的学生中,已知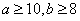
正确答案
见解析。
解析
(1)依题意,最先检测的3个人的编号依次为785,667,199;
(2)由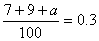
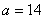
∵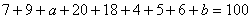
∴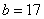
(3)由题意,知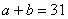
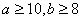
∴满足条件的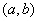
(17,14),(18,13),(19,12),(20,11),(21,10),(22,9),(23,8)共14组,
且每组出现的可能性相同.
其中数学成绩为优秀的人数比及格的人数少有:
(10,21),(11,20),(12,19),(13,18),(14,17),(15,16)共6组.
∴数学成绩为优秀的人数比及格的人数少的概率为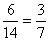
知识点
为了调查我市在校中学生参加体育运动的情况, 从中随机抽取了16名男同学和14名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率, 从我市中学生中随机抽取3人,若其中喜爱运动的人数为

正确答案
见解析。
解析
(1)
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关
(3)统计结果中喜爱运动的中学生所占的频率为
喜爱运动的人数为


喜爱运动的人数为
因为


知识点
某公司为招聘新员工设计了一个面试方案:应聘者从






(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
正确答案
见解析
解析
(1)设甲正确完成面试的题数为





考生甲正确完成题数

设乙正确完成面试的题数为






考生乙正确完成题数

(2)因为

(或
所以
(或:因为

所以
综上所述,
从做对题数的数学期望考查,两人水平相当;
从做对题数的方差考查,甲较稳定;
从至少完成
知识点
“光盘行动”倡导厉行节约,反对铺张浪费,带动大家珍惜粮食,吃光盘子中的食物,得到从中央到民众的支持,为了解某地响应“光盘行动”的实际情况,某校几位同学组成研究性学习小组,从某社区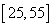
(1)求a,b的值,并估计本社区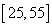
(2)从年龄段在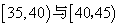
(1)已知选取2人中1人来自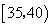
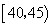
(2)求2名领队的年龄之和的期望值(每个年龄段以中间值计算).
正确答案
见解析。
解析
(1)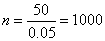
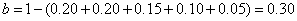
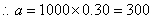
样本中的“光盘族”人数为
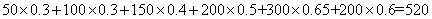
样本中“光盘族”所占比例为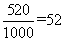
(2)(ⅰ)记事件A为“其中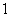
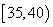
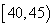
所以概率为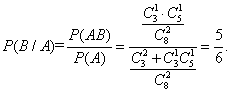
(ⅱ)设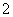
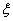
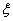
所以 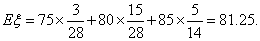
知识点
扫码查看完整答案与解析