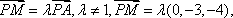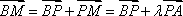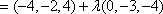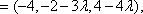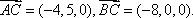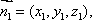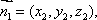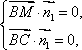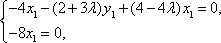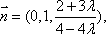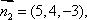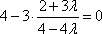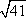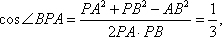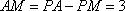- 直线、平面垂直的综合应用
- 共97题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图5,在直棱柱
(1)证明:
(2)求直线
正确答案
见解析
解析
1(1)
如图,因为







(2I)因为



连结









由(I)可知:


在直角梯形ABCD中,因为








在


即直线

解法2. (I)
易知AB,AD,








从而


因为



于是




(2)由(I)知







设直线



即直线

知识点
函数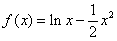
正确答案
解析
略。
知识点
如图,设

正确答案
解析
略
知识点
已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)·(sin A-sin B)=(c-b)sin C,则△ABC面积的最大值为________。
正确答案
解析
知识点
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)证明:∠D=∠E;
(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形。
正确答案
见解析。
解析
(1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE.由已知得∠CBE=∠E,故∠D=∠E.
(2)设BC的中点为N,连接MN,则由MB=MC知MN⊥BC,故O在直线MN上。
又AD不是⊙O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD,
所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E,由(1)知,∠D=∠E,所以△ADE为等边三角形。
知识点
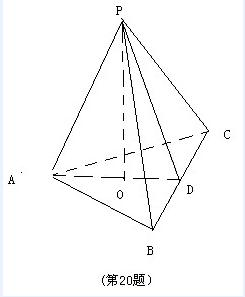
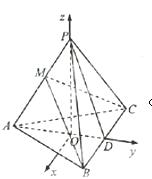
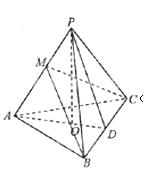
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。
正确答案
见解析
解析
(1)证明:如图,以O为原点,以射线OP为z轴的正半轴,建立空间直角坐标系O-xyz
则O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0)
P(0,0,4)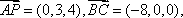
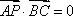
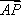

(2)解:设
设平面BMC的法向量
平面APC的法向量
由
得
即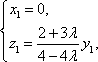
由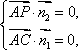
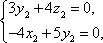
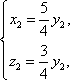
由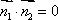
解得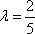
综上所述,存在点M符合题意,AM=3。
方法二:
(1)证明:由AB=AC,D是BC的中点,得AD⊥BC,
又PO⊥平面ABC,得PO⊥BC。
因为PO∩BC=0,所以BC⊥平面PAD
故BC⊥PA.
(2)解:如图,在平面PAD内作BM⊥PA于M,连CM.
由(Ⅰ)中知AP⊥BC,得AP⊥平面BMC.
又AP
在Rt⊿ADB中,AB2=AD2+BD2=41,得AB=
在Rt⊿POD中, PB2=PO2+OD2,
在Rt⊿PDB中, PB2=PD2+BD2,
所以PB2=PO2+OD2+BD2=36,得PB=6.
在Rt⊿POA中, PA2=AO2+OP2=25,得PA=5
又
从而
综上所述,存在点M符合题意,AM=3.
知识点
若某程序图如图所示,则该程序运行后输出的k的值是 。
正确答案
5
解析













知识点
在

正确答案
解析
因为


即





知识点
4.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析