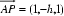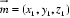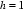- 平面与平面垂直的判定与性质
- 共123题
19.如图,已知长方形














二面角

正确答案
(1)证明:
∵长方形ABCD中,AB=

∴AM=BM
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM⊂平
∴BM⊥平面ADM ∵AD⊂平面ADM ∴AD⊥BM;
(2)建立如图所示的直角坐标系,设




设平面AME的一个法向量为

所以
因

求得
解析
已知面面垂直,得到线线垂直。建立空间直角坐标系计算求得
考查方向
面面垂直的性质定理,二
解题思路
求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的
易错点
计算能力,找二面角的平面角
知识点
19.如图,四棱柱








(Ⅰ)证明:平面

(Ⅱ)若

正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(Ⅰ)依题意
∴

∵









(Ⅱ)连接


故以






设面


令



同理可求出面

故



考查方向
本题考查了立体几何中的面面垂直和二面角的问题.属于高考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
1、转化为证明线面垂直。
2、建立空间直角坐标系,利用夹角的余弦公式求解。
易错点
1、第一问中的面面垂直的转化。
2、第二问中二面角求解时要建立适当的空间直角坐标系。
知识点
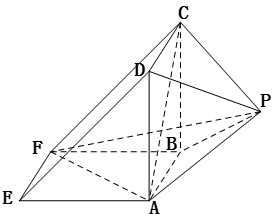
19. 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=
(Ⅰ)若M为EA中点,求证:AC∥平面MDF;
(Ⅱ)求平面EAD与平面EBC所成锐二面角的大小.
正确答案
(1)略;(2)60O.
解析
⑴证明:设



在矩形


因为

所以

又因为



所以

⑵解:因为平面






所以

以
设


因为
所以

设平面




注意到平面

所以,平面


考查方向
本题考查了立体几何中的线面平行和二面角的问题.属于高考中的高频考点。
解题思路
1、转化为证明线线平行
2、建立空间直角坐标系,利用夹角的余弦公式求解。
易错点
1、第一问中的线面平行的转化。
2、第二问中二面角求解时要建立适当的空间直角坐标系。
知识点
18.如图所示,该几何体是由一个直三棱柱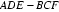
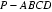
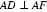
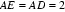
(1)证明:平面
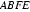
(2)求正四棱锥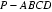


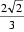
正确答案
(1)略;
(2)1
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)证明:直三棱柱

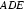
所以: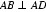

所以:
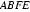
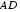
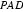
所以:平面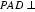
(2)由(2)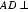
以
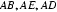
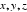
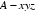
设正四棱锥

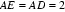
则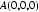
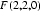
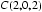
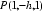
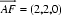
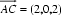
设平面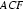
则: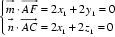
取
则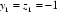
所以:
设平面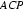

则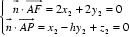
取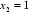
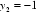
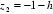
所以: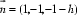

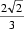
所以,
解得:
考查方向
本题考查了立体几何中的面面垂直和二面角的问题.属于高考中的高频考点。
解题思路
本题考查导数的性质,解题步骤如下:
1、转化为证明线面垂直。
2、建立空间直角坐标系,利用夹角的余弦公式求解。
易错点
1、第一问中的面面垂直的转化。
2、第二问中二面角求解时要建立适当的空间直角坐标系。
知识点
17.如图,在四棱锥










(Ⅰ)求证:

(Ⅱ)若



(Ⅲ)如果直线




正确答案
(Ⅰ)证明略;
(Ⅱ)证明略;
(Ⅲ)
解析
试题分析:本题属于立体几何的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意判定定理的条件要全
(Ⅰ)证明:在平行四边形


所以
由


所以
因为侧面


所以

又因为

所以
又因为




所以

(Ⅱ)证明:因为



所以
又因为



所以

同理,得

又因为




所以平面

又因为

所以

(Ⅲ)解:因为



分别为


则
所以


设

所以

易得平面

设平面

由

令

因为直线


所以

所以 
解得

考查方向
本题主要考查了空间中直线与平面的位置关系的转化、空间向量在立体几何中的运用;空间中线面位置关系的证明值域有以下几类:
1.线线间的平行或垂直,
2.面面间的平行或垂直,
3.线面间的平行或垂直;
空间向量在立体几何中的运用,主要分以下几类:
1.利用空间向量求异面直线的角,
2.利用空间向量求直线与平面所成的角,
3.利用空间向量求二面角,
4.利用空间向量求点到平面的距离.
解题思路
本题考查立体几何问题,解题步骤如下:
1.利用线面垂直的判定定理进行证明;
2.利用三角形的中位线得到线线平行,利用线面平行的判定定理得到线面平行;
3.利用面面平行的判定定理进行证明;
4.建立空间直角坐标系,利用三点共线设点,求出平面的法向量;5.利用两角相等求得比值。
易错点
1、第一、二问中,利用判定定理证明时,条件不全;
2、第三问中写点的坐标出现错误。
知识点
扫码查看完整答案与解析