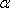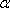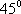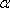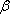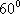- 平面与平面垂直的判定与性质
- 共123题
在空间中,过点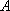
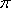
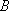
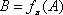
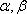
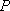
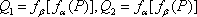
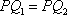
正确答案
解析
设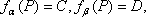
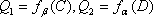
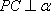
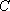
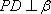
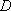
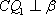
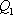
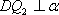
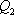
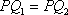
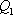
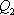
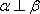
知识点
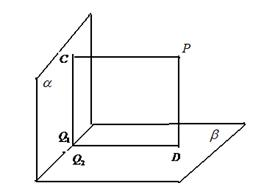
如图,正方形







(1)当点



(2)当平面



正确答案
见解析。
解析
(1)以直线





则




又



∴


(2)设

设


设



取

又由题设,

∴ 
即点




∴ 
知识点
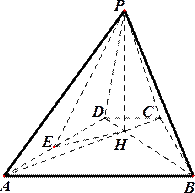
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点。
(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值。
正确答案
见解析。
解析
以H为原点,HA、HB、HP分别为x、y、z轴,线段
HA的长为单位长,建立空间直角坐标系如图,
则A(1,0,0),B(0,1,0)。
(1)设C(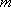

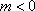
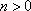
则D(0,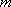

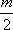
可得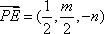
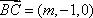
因为
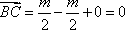
(2)由已知条件可得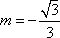
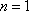
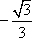
D(0,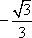

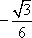
设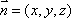
则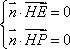
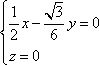
因此可以取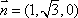
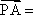
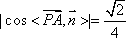
所以直线PA与平面PEH所成角的正弦值为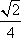
知识点
如图,在三棱锥









求证:(1)平面

(2)
正确答案
见解析。
解析
证明:(1)∵

∵E.F分别是SA.SB的中点 ∴EF∥AB
又∵EF

同理:FG∥平面ABC
又∵EF


(2)∵平面




∴AF⊥平面SBC 又∵BC
又∵



知识点
已知点G为ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且


正确答案
解析
M、G、N三点共线
又G为ABC的重心
知识点
扫码查看完整答案与解析