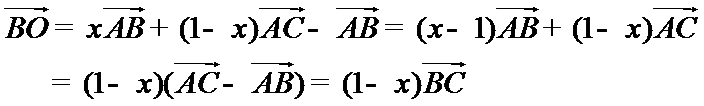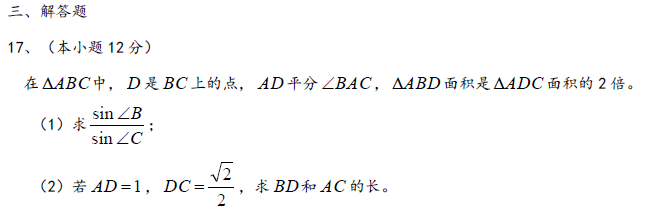三角形中的几何计算
共100题

· 三角形中的几何计算

三角形中的几何计算
共100题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

17.在中，角的对边分别为，且，.

（1）求角B的大小；

（2）若等差数列的公差不为零，且=1，且成等比数列，求的前项和.

正确答案

（1）；

（2）.

解析

试题分析：本题第（1）问属于解三角形以及三角恒等变换的知识，是基础知识，难度中等；第（2）问是数列求和的问题，用主要考查了裂项相消法求数列的前n项和，解答过程如下：

（Ⅰ）由，所以，又，再由得

，即，，则为钝角。

，则，

解得。

（Ⅱ）设的公差为，由已知得，且.

∴ ．

又, ∴. ∴.

∴. ∴ .

考查方向

本题考查了解三角形以及数列的相关问题，主要考查了余弦定理、三角恒等变换、等差、等比数列的性质以及数列求和等知识，同时考查了转化化归思想以及运算求解能力。

解题思路

1、第（1）问根据余弦定理求出，然后再利用已知条件以及三角恒等变换公式进行转化求解即可。

2、第（2）问可以先用已知条件求出，然后利用裂项相消法求数列的前n项和。

易错点

本题容易因为忽略三角形内角的范围而导致错误的出现。

知识点

三角形中的几何计算

题型：填空题

填空题 · 5 分

14．在Rt△ABC中，∠A＝90°，AB＝AC＝2，点D为AC中点，点E满足，则＝．

正确答案

-2

解析

所以

考查方向

本题主要考查向量的线性运算、平面向量基本定理以及向量的数量积等知识，意在考查考生的运算能力和逻辑推理能力。

解题思路

1.先将向量分别用向量表示出来；

2.利用数量积运算求出所求答案。

易错点

1.不会将所求的向量都用基底表示出来；

2.向量的数量积运算律和实数的运算混淆。

知识点

三角形中的几何计算

题型：单选题

单选题 · 5 分

7．在中，点在线段上，且，点在线段上(与点不重合).若，则的取值范围是( )

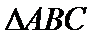
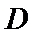
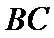
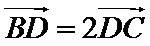
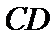
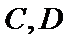
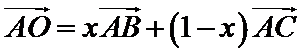
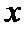
正确答案

解析

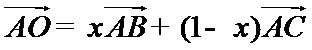
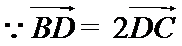
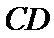
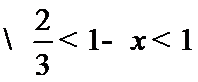
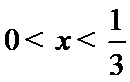
如图,由有

且点在线段上(与点不重合)，

，解得.

A选项不正确，B选项不正确，D选项不正确，所有选C选项.

考查方向

本题主要考查了平面向量的基本运算.

解题思路

1、通过，将其中的向量统一用向量来表示. 2、利用进一步构造关于的数量关系.即可得到结果.

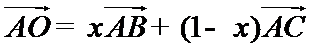
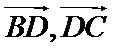
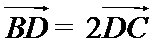
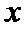
A选项不正确，B选项不正确，D选项不正确，所有选C选项.

易错点

1、本题易在平面向量的加法和减法的运算规律上出错，将二者的运算法则混淆. 2、本题不容易找出各向量之间的联系，从而使题解无法进行.

知识点

三角形中的几何计算

题型：单选题

单选题 · 5 分

9.在△ABC中，内角A，B，C 所对的边分别为 a，b，c，若 cos 2B＋cosB＝1－cos AcosC 则（）

Aa，b，c 成等差数列

Ba，b，c 成等比数列

Ca，2b，3c 成等差数列

Da，2b，3c 成等比数列

正确答案

解析

由cos 2B＋cosB＝1－cos AcosC

得到sin 2B=cos Acos C－cos（A＋C）

所以sin 2B=cos Acos C－cos AcosC＋sinAsinC

所以sin 2B=sinAsinC

由正弦定理得，b2 = ac，所以a，b，c 成等比数列，故选B。

考查方向

本题主要考查等比中项、同角三角函数的基本关系、两角和与差的余弦公式、正弦定理等知识，意在考查考生的运算推理能力。

解题思路

1.先利用三角函数中的公式将cos 2B＋cosB＝1－cos AcosC化简；

2.利用正弦定理得到边之间的关系即可。

易错点

1.对于题中cos 2B＋cosB＝1－cos AcosC的化简不会入手；

2.对于三角函数的化简出错

知识点

三角形中的几何计算等差数列的判断与证明等比数列的判断与证明

题型：简答题

简答题 · 12 分

正确答案

知识点

正弦定理的应用余弦定理的应用三角形中的几何计算

继续学习学习下一知识点

下一知识点 : 解三角形的实际应用

百度题库 > 高考 > 理科数学 > 三角形中的几何计算

扫码查看完整答案与解析