- 三角形中的几何计算
- 共100题
17.△ABC的内角A,B,C的对边分别别为a,b,c,已知
(I)求C;
(II)若

正确答案
解(Ⅰ)∵2cos C(acosB+bcosA)=C
∴2cos C(sinAcos B+sinBcosA)=sinC
∴2cosC sin(A+B)=sinC
∴2cosC sinC=sin C
∴ 0<C<π
∴ cosC= 
∴ C= 
(Ⅱ) ∵△ABC面积为
∴
∴(a+b)2=a2+b2+2ab=13+12=25
∵a+b=5
∴a+b+c=5+
∴
知识点
在


(Ⅰ)证明:
(Ⅱ)若

正确答案
(I)由正弦定理得
故
于是
又




因此

所以,
(II)由


因

又


当

当

综上,

知识点
16.(本小题满分12分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知
(Ⅰ)证明:a+b=2c;
(Ⅱ)求cosC的最小值.
正确答案
解析:

化简得
即
因为
所以
从而
由正弦定理得



所以 
当且仅当
故 

考查方向
两角和的正弦公式、正切公式、正弦定理、余弦定理及基本不等式.
教师点评
知识点
(本小题满分12分)
在△ABC中,角A,B,C所对的边分别是a,b,c,且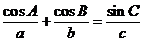
(I)证明: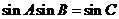
(II)若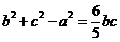
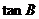
正确答案
(Ⅰ)根据正弦定理,可设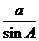
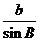
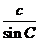
则a=ksin A,b=ksin B,c=ksin C.
代入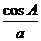
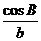
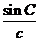
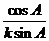
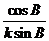
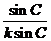
sin Asin B=sin Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π–C)=sin C,
所以sin Asin B=sin C.
(Ⅱ)由已知,b2+c2–a2=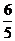
cos A=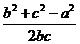
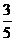
所以sin A=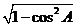

由(Ⅰ),sin Asin B=sin Acos B+cos Asin B,
所以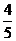
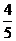
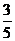
故tan B=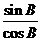
知识点
(14分)(2015•上海)如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
(1)求t1与f(t1)的值;
(2)已知警员的对讲机的有效通话距离是3千米.当t1≤t≤1时,求f(t)的表达式,并判断f(t)在[t1,1]上的最大值是否超过3?说明理由.
正确答案
解:(1)由题意可得t1=

设此时甲运动到点P,则AP=v甲t1=5×

∴f(t1)=PC=
=

(2)当t1≤t≤
∴QB=AC+CB﹣8t=7﹣8t,PB=AB﹣AP=5﹣5t,
∴f(t1)=PC=
=

(2)当t1≤t≤
∴QB=AC+CB﹣8t=7﹣8t,PB=AB﹣AP=5﹣5t,
∴f(t)=PQ=
=
=
当
∴f(t)=PB=AB﹣AP=5﹣5t
∴f(t)=
∴当

故f(t)的最大值超过了3千米.
知识点
扫码查看完整答案与解析















