- 复合函数的单调性
- 共394题
已知函数



(1)求

(2)如果当



正确答案
见解析
解析
(1)

(2)由(1)知
设
①如果



故,由当
从而,当

②如果

而


③如果





综合以上情况可得:
知识点
设函数
(1)求函数
(2)当


正确答案
见解析。
解析
(1)
由



又∵

∴函数

(2)

∵

由


由


当




∴在区间
当当



∴在区间
知识点
已知向量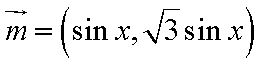

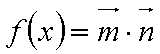
(1)求函数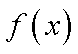
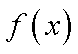
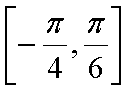
(2)在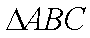
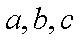
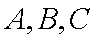
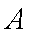
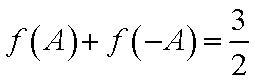
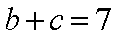
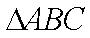
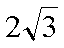
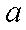
正确答案
见解析。
解析
(1)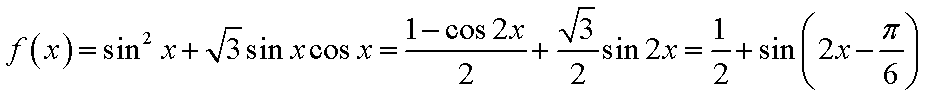
因为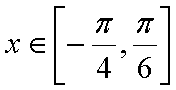
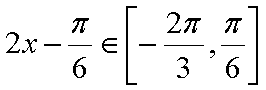
所以当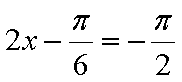

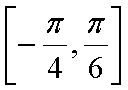
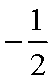
(2)由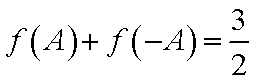
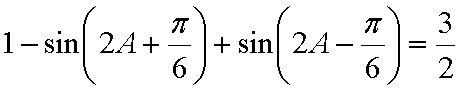
化简得: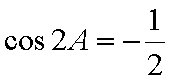
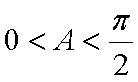
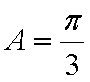
由题意知: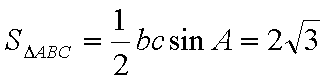
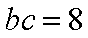
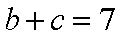
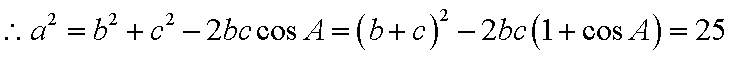
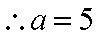
知识点
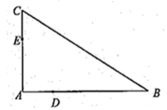
如图,D,E分别为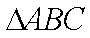
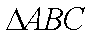
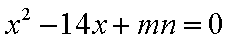
(1)证明:C,B,D,E四点共圆;
(2)若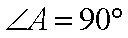
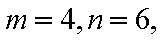
正确答案
见解析
解析
解析:解:
(1)连接DE,根据题意在△ADE和△ACB中,
AD×AB=mn=AE×AC,
即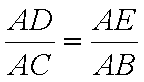
因此∠ADE=∠ACB
所以C,B,D,E四点共圆。
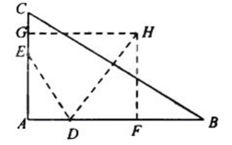
(2)m=4, n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.
故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF= 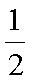
故C,B,D,E四点所在圆的半径为5
知识点
已知函数






(1)求
(2)将函数






正确答案
(1)
解析
解析:(1)
-------------------------------------------3分
由题意知,最小正周期


∴
(2)将




令







∴

知识点
已知函数
(1)若f(x)≤ m的解集为{x|—1≤x≤5),求实数a,m的值;
(2)当a=2且0≤t<2时,解关于x的不等式f(x)+t≥f(x+2)。
正确答案
见解析
解析
解析:(1)
(2)
知识点
已知函数
(1)函数
(2)写出函数
正确答案
见解析。
解析
(1)
函数
∵



(2)

令
∴函数

知识点
设a为锐角,若cos(a+


正确答案
解析
∵ a为锐角,cos(a+

∴ a+


∴ cosa=cos[(a+





sina=sin[(a+





由此可得sin2a=2sinacosa=
又∵ sin




∴ sin(2a+






故答案为:
知识点
在△ABC中,


(1)判断△ABC的形状;
(2)若

正确答案
(1)等腰三角形(2)
解析
(1)由
∴








(2)∵ 






知识点
已知函数
(1)当

(2)当


正确答案
见解析
解析
(1)解:原不等式可化为
当


当



当



综上所述:原不等式的解集为
(2)原不等式可化为
∵

即
故

当




∴实数

知识点
扫码查看完整答案与解析