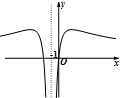
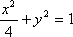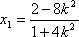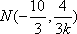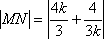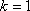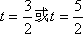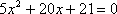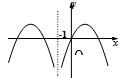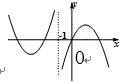- 复合函数的单调性
- 共394题
某人沿一条折线段组成的小路前进,从








试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号)。
正确答案
见解析
解析
示意图,如图所示,
连接AC,在△ABC中,∠ABC=50°+(180°-110°)=120°,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得
在△ACD中,∠ACD=360°-140°-(70°+30°)=120°,CD=3
由余弦定理得AD=
=

由正弦定理得sin∠CAD=
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°,
所以,从A到D的方位角是125°,距离为
知识点
数列










(2)设




正确答案
见解析
解析
(1)∵



当


当



∴数列



设




(2)
∴

∴

∴数列

综上所述,
知识点
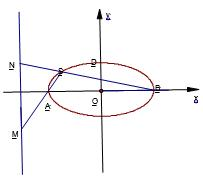
已知椭圆C的左,右焦点坐标分别为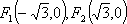
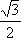

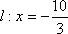
(1)求椭圆C的方程;
(2)求线段MN长度的最小值;
(3)当线段MN的长度最小时,在椭圆C上的T满足:

正确答案
(1)椭圆C的方程为
(2)
(3)T的个数是2
解析
(1)因为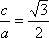
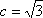
所以椭圆C的方程为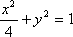
(2)易知椭圆C的左,右顶点坐标为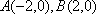
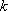
故可设直线AS的方程为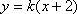
由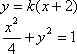
设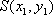
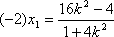
从而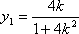
又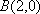
由
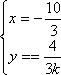
故
又
当且仅当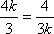

所以

(3)由(2)知,当线段MN的长度取最小值时,
此时AS的方程为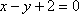
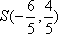
所以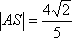


只需点T到直线AS的距离等于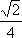
所以点T在平行于AS且与AS距离等于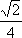
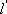
设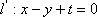
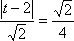
① 当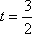
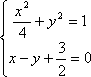
由于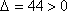
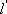
②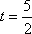
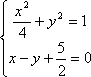
由于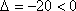
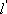
综上所求点T的个数是2. ……………………………………………..14分
知识点
若函数


(1)判断下列函数:①

(2)证明:对任意的正奇数

(3)证明:任意的

正确答案
见解析
解析
(1)①②都是等比源函数.
(2)证明:假设存在正整数




等式两边同除以

因为
所以等式
所以假设不成立,说明对任意的正奇数

(3)因为任意的

所以任意的



由



令

所以
所以任意的


所以任意的

知识点
下列四个图中,函数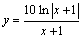
正确答案
解析
略
知识点
扫码查看完整答案与解析