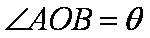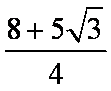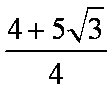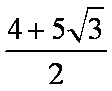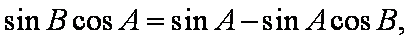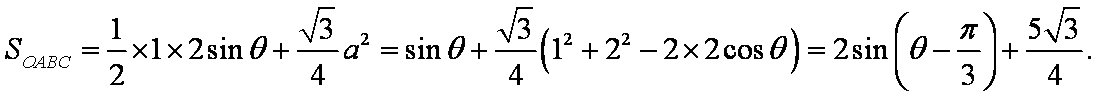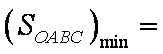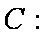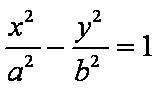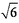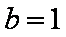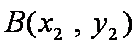- 复合函数的单调性
- 共394题
如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点。
(1)如果A,B两点的纵坐标分别为

(2)在(1)的条件下,求cos(β﹣α)的值;
(3)已知点C

正确答案
见解析
解析
(1)根据三角函数的定义,得

又α是锐角,所以,
(2)由(1)知,

又α是锐角,β是钝角,
所以

所以
(3)由题意可知,

所以
因为

所以函数

知识点
已知
(1)当a=1时求不等式
(2)如果函数
正确答案
见解析。
解析
(1)
∴

(2)由

令


这两个函数的图象有两个不同的交点,
所以,函数
知识点
在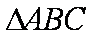
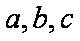
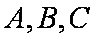
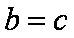
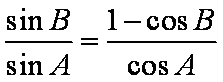
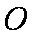
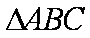
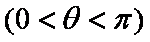
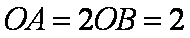
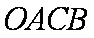
正确答案
解析
由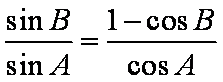
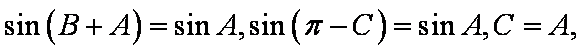
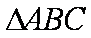
设该三角形的边长为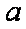
显然当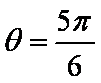
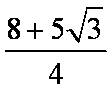
知识点
如图,已知抛物线










(1)求抛物线
(2)当

求直线
(3)若直线



正确答案
见解析
解析
(1)∵点

∴


(2)法一:∵当



设

∴

∴

法二:∵当







联立方程组

∵
∴

同理可得


(3)法一:设


可得,直线

同理,直线

∴

∴直线

令

∵


∴
法二:设点


以


⊙

①-②得:
直线

当



∵


∴
知识点
已知函数 f(x)=ax+x﹣b的零点xb∈(n,n+1)(n∈Z),其中常数a,b满足2a=3,3b=2,则n的值是( )
正确答案
解析
∵2a=3,3b=2,∴a=log23,b=log32,
∴函数f(x)=(log23)x+x﹣log32,且函数是R上的增函数,
而f(﹣1)=﹣1<0,f(0)=1﹣log32>0,
∴函数f(x)=(log23)x+x﹣log32在(﹣1,0)内有一个零点,
故n=﹣1,
故选B。
知识点
已知双曲线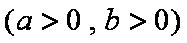
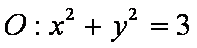
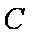
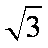

(1)求双曲线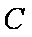
(2)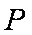

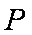

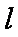
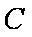
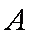
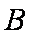
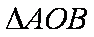
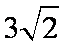
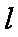
正确答案
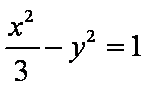
(1)
解析
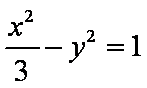
1)∵双曲线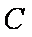

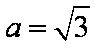
过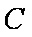
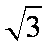

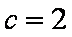
故双曲线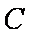
(2)设直线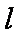
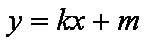
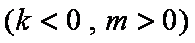
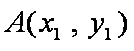
圆心
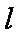
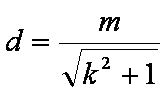
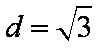
由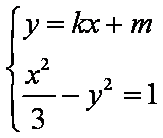
则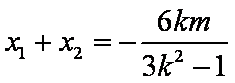
又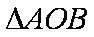
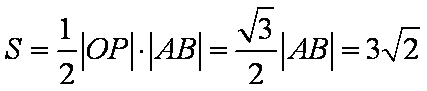
由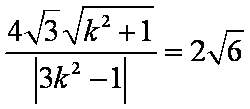
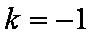
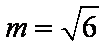
知识点
一个口袋内有



(1)当


(2)若



正确答案
见解析
解析
(1)法一:
白球的个数


法二:白球个数

(2)由题设知,
因为

解不等式得,
又因为


所以


知识点
已知函数y=f(x)是定义在R上的奇函数,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0(其中f′(x)是f(x)的导函数),若a=(30.3)•f(30.3),b=(logπ3)•f(logπ3),
c=(log3

正确答案
解析
解:令F(x)=xf(x),则F′(x)=f(x)﹣xf′(x)。
因为f(x)+xf′(x)<0,
所以函数F(x)在x∈(﹣∞,0)上为减函数。
因为函数y=x与y=f(x)都是定义在R上的奇函数,
所以函数F(x)为定义在实数上的偶函数。
所以函数F(x)在x∈(0,+∞)上为增函数。
又30.3>30=1,0=logπ1<logπ3<logππ=1,
则F(|
所以(log3

即c>a>b。
故选C,
知识点
正方体ABCD﹣A1B1C1D1棱长为1,平面α垂直于体对角线BD1,则该正方体在平面α上射影的面积是( )
正确答案
解析
解:如图示,由题意知,
BD1⊥A1D,BD1⊥C1D,A1D∩C1D=D,
则平面A1C1D即为平面α
则该正方体在平面α上射影的面积即为:△A1AD,△A1C1B1,△CC1D在平面A1C1D上投影的面积再加上△A1C1D的面积
而△A1AD≌△A1C1B1≌△CC1D,且△A1AD≌△A1D1D,
故△A1AD,△A1C1B1,△CC1D在平面A1C1D上投影的面积为三倍的△A1D1D在平面A1C1D上投影的面积
而三倍的△A1D1D在平面A1C1D上投影的面积即为△A1C1D的面积
故该正方体在平面α上射影的面积为


故选B
知识点
已知函数
(1)当

(2)当


正确答案
(1)
解析
(1)
①当
②当

③当
综上,不等式的解集为
(2)即


知识点
扫码查看完整答案与解析