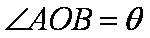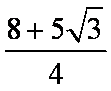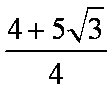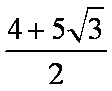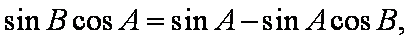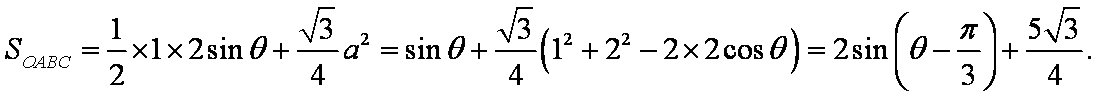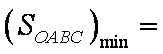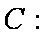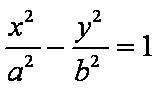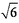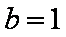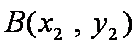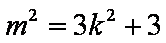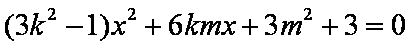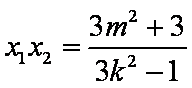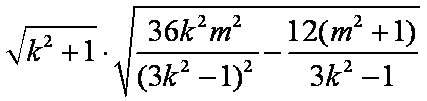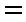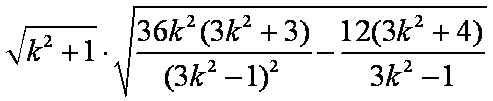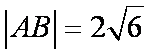- 复合函数的单调性
- 共394题
在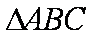
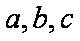
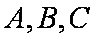
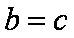
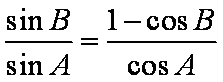
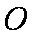
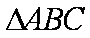
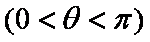
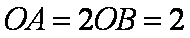
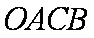
正确答案
解析
由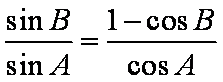
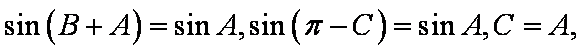
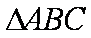
设该三角形的边长为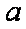
显然当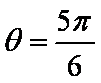
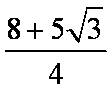
知识点
如图,已知抛物线










(1)求抛物线
(2)当

求直线
(3)若直线



正确答案
见解析
解析
(1)∵点

∴


(2)法一:∵当



设

∴

∴

法二:∵当







联立方程组

∵
∴

同理可得


(3)法一:设


可得,直线

同理,直线

∴

∴直线

令

∵


∴
法二:设点


以


⊙

①-②得:
直线

当



∵


∴
知识点
已知双曲线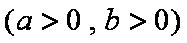
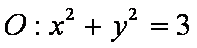
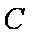
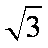

(1)求双曲线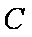
(2)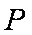

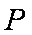

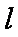
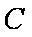
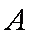
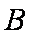
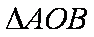
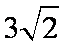
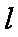
正确答案
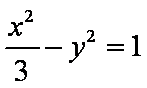
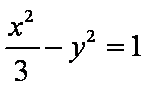
(1)
解析
1)∵双曲线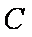

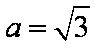
过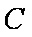
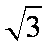

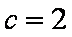
故双曲线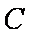
(2)设直线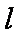
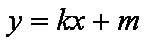
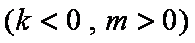
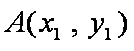
圆心
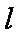
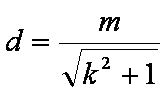
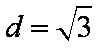
由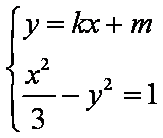
则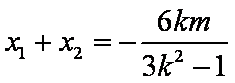
又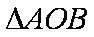
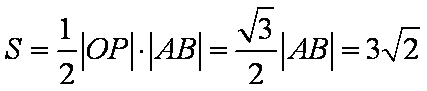
由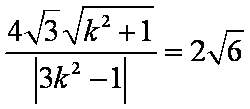
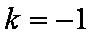
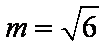
知识点
一个口袋内有



(1)当


(2)若



正确答案
见解析
解析
(1)法一:
白球的个数


法二:白球个数

(2)由题设知,
因为

解不等式得,
又因为


所以


知识点
已知函数
(1)当

(2)当


正确答案
(1)
解析
(1)
①当
②当

③当
综上,不等式的解集为
(2)即


知识点
扫码查看完整答案与解析