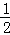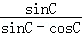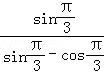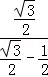- 复合函数的单调性
- 共394题
下列函数中,在(0,+∞)上单调递增的偶函数是( )
正确答案
解析
:y=cosx是偶函数,但在(0,+∞)上有增有减,故排除A;
y=x3在(0,+∞)上单调递增,但为奇函数,故排除B;
y=y=
y=ex+e﹣x是偶函数,由于y′=ex﹣e﹣x,在(0,+∞)上,y′>0,故其在(0,+∞)上单调递增的;正确。
故选D。
知识点
已知函数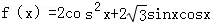
(1)求函数f(x)的最小正周期;
(2)在△ABC中,若f(C)=2,2sinB=cos(A﹣C)﹣cos(A+C),求tanA的值。
正确答案
见解析。
解析
(1)函数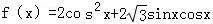
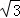
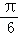
∴函数的最小正周期为: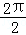
(2)∵f(C)=2,∴2sin(2C+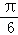
∴sin(2C+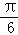
∵0<C<π,
∴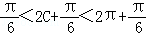
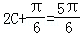
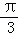
∵2sinB=cos(A﹣C)﹣cos(A+C)=2sinAsinC,
∴sin(A+C)=sinAsinC,
即:sinAcosC+cosAsinC=sinAsinC,
即:tanA=
=
=
=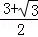
知识点
已知函数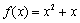
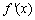
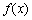
(1)若数列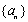
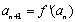
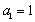
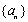
(2)若数列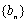
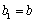
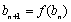
(ⅰ)是否存在实数
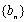
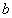
在,请说明理由;
(ⅱ)若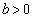
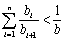
正确答案
见解析
解析
(1)解:因为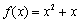
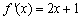
所以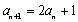
所以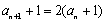
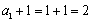
所以数列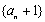
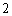
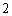
所以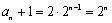
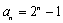
(2)
(ⅰ)证明:假设存在实数
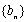
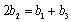
且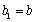
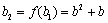

所以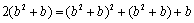
解得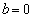

当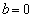
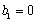
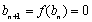
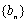
当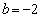


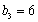
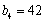
所以,当
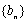
(ⅱ)证明: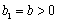
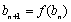
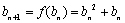
所以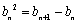
所以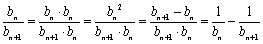
因为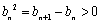
所以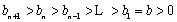
所以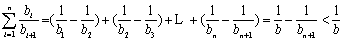
知识点
某工厂生产的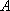

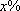

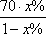

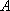

正确答案
解析
略
知识点
已知函数



正确答案
解析
略
知识点
扫码查看完整答案与解析