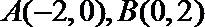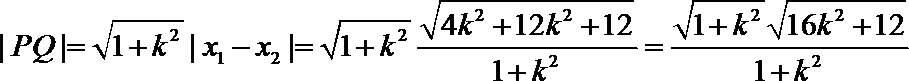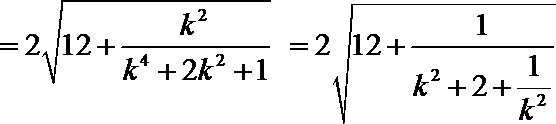- 复合函数的单调性
- 共394题
5.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
②标准差
③平均数

④平均数
⑤众数等于1且极差小于或等于1。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,椭圆




(1)求椭圆的方程;
(2)设






(I)若

(II)求证:
正确答案
(1)由题设知
由点(1,e)在椭圆上,得
解得

又点


因此,所求椭圆的方程是
(2) 由(1)知




直线

由

故
同理, 
(ⅰ)由①②得

因为


(ⅱ)因为直线


故
从而
因此
又由①②知
所以

解析
解析已在路上飞奔,马上就到!
知识点
9.不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
27.已知圆C经过点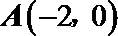
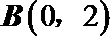
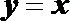
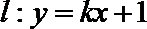
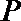

(I)求圆C的方程;
(II)若
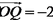
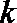
(III)过点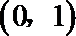

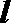
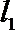
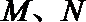

正确答案
(I)设圆心
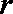
所以
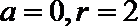
所以圆
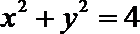
(II)方法一:
因为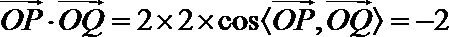
所以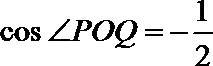
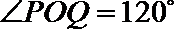
所以圆心到直线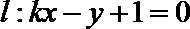
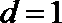
又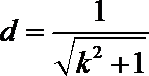
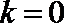
方法二:设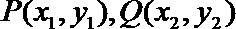
因为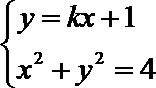
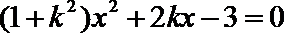
由题意得:
因为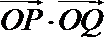
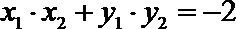
又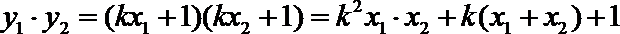
所以, 
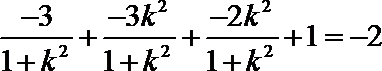
化简得: 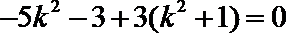
所以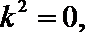
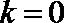
(III)方法一:
设圆心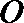
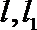

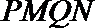
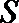
因为直线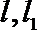
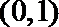
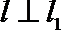
根据勾股定理,有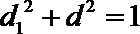
又根据垂径定理和勾股定理得到,
而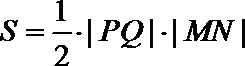
当且仅当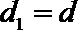
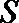
方法二:设四边形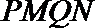
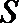
当直线
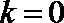

此时
当直线

设
则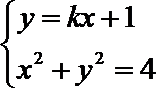
所以
同理得到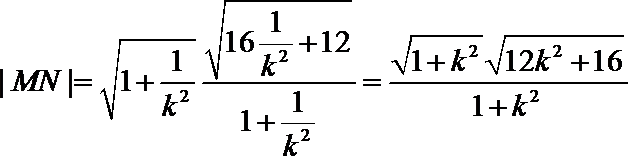
因为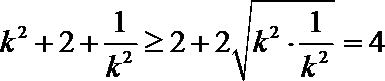
所以 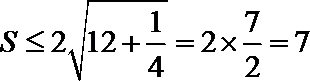
当且仅当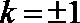
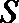

解析
解析已在路上飞奔,马上就到!
知识点
12.设



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
4. 在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析