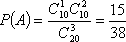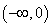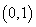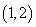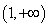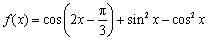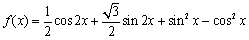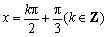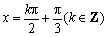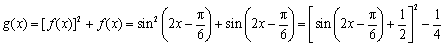- 复合函数的单调性
- 共394题
若直线



正确答案
解析
略
知识点
已知


正确答案
解析
略
知识点
某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量



(1)试求药量峰值(

(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
正确答案
(1)1小时(2)
解析
(1)由曲线过点


当

当





综上可知


所以药量峰值为4mg,达峰时间为1小时。 ……………………6分
(2)当


解得


当


由


又



由图像知当


∵
所以成人按规定剂量服用该药一次后能维持大约
知识点
如图,程序框图所进行的求和运算是
正确答案
解析
略
知识点
把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图象是( )
正确答案
解析
将函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
得到的图象对应的解析式为:y=cosx+1,
再将y=cosx+1图象向左平移1个单位长度,再向下平移 1个单位长度,
得到的图象对应的解析式为:y=cos(x+1),
∵曲线y=cos(x+1)由余弦曲线y=cosx左移一个单位而得,
∴曲线y=cos(x+1)经过点(



由此可得,A选项符合题意。
故选A
知识点
今年雷锋日,某中学从高中三个年级选派4名教师和20名学生去当雷锋志愿者,学生的名额分配如下:
(1)若从20名学生中选出3人参加文明交通宣传,求他们中恰好有1人是高一年级学生的概率;
(2)若将4名教师安排到三个年级(假设每名教师加入各年级是等可能的,且各位教师的选择是相互独立的),记安排到高一年级的教师人数为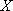
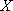
正确答案
见解析
解析
(1)设“他们中恰好有1人是高一年级学生”为事件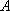
答:若从选派的学生中任选3人进行文明交通宣传活动,他们中恰好有1人是高一年级学生的概率为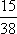
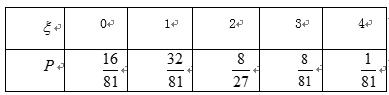
(2)解法1: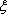

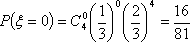
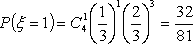
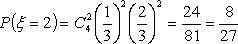
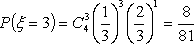

随机变量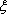
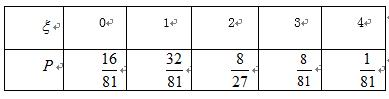
所以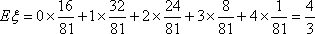
解法2:由题意可知,每位教师选择高一年级的概率均为
则随机变量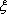

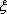
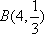
随机变量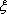
所以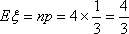
知识点
已知函数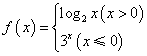
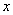
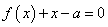
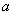
正确答案
解析
略
知识点
已知数列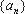

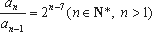
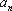

正确答案
6或7
解析
略
知识点
已知点







(1)求动点

(2)已知圆










正确答案
(1)
(2)
解析
(1)设


即




(2)设圆


圆



令


由①、②解得,


∴

∴

当

当且仅当


故当


知识点
已知函数
(1)求函数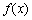
(2)设函数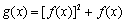
正确答案
见解析
解析
(1)
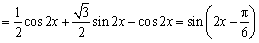
∴最小正周期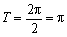
由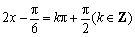
函数图象的对称轴方程为
(2)
当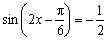
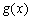
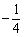
当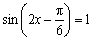
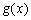
所以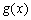
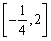
知识点
扫码查看完整答案与解析