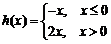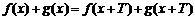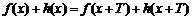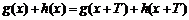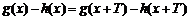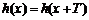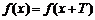复合函数的单调性
共394题

· 复合函数的单调性

复合函数的单调性
共394题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

已知函数的图像是由函数的图像经如下变换得到：先将图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移个单位长度.

22.求函数的解析式，并求其图像的对称轴方程；

23.已知关于的方程在内有两个不同的解．

（1）求实数m的取值范围；

（2）证明：

第(1)小题正确答案及相关解析

正确答案

（Ⅰ），

解析

（1）将的图像上所有点的纵坐标伸长到原来的2倍（横坐标不变）得到的图像，再将的图像向右平移个单位长度后得到的图像，故，从而函数图像的对称轴方程为

考查方向

1、三角函数图像变换和性质；2、辅助角公式和诱导公式．

解题思路

有函数的图象变化规律可得到函数的本来面貌，从而求得对称轴方程。

易错点

三角函数变换过程中参数的变换掌握不好，计算能力弱

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）（1）；（2）详见解析．

解析

（2）1）

（其中）

依题意，在区间内有两个不同的解当且仅当，故m的取值范围是.

2）因为是方程在区间内有两个不同的解，

所以，.

当时，

当时,

所以

考查方向

1、三角函数图像变换和性质；2、辅助角公式和诱导公式．

解题思路

结合函数图象，化简三角函数，然后建立不等关系，求出M的取值范围

易错点

计算能力弱，三角函数的图象变换和性质掌握不好，不会利用辅助角公式和诱导公式。

题型：单选题

单选题 · 5 分

18. 设是定义域为的三个函数，对于命题:①若，，均为增函数，则中至少有一个为增函数；②若，，均是以为周期的函数，则均是以为周期的函数，下列判断正确的是( )

A①和②均为真命题

B①和②均为假命题

C①为真命题，②为假命题

D①为假命题，②为真命题

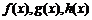
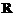
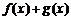
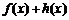
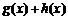
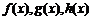
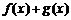
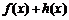
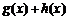
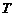
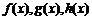
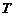
正确答案

解析

①不成立，可举反例

, ,

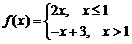
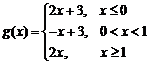
②

前两式作差，可得

结合第三式，可得,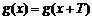

也有

∴②正确

故选D

知识点

复合函数的单调性函数的周期性

题型：简答题

简答题 · 12 分

21.设函数f（x）=acos2x+（a-1）（cosx+1），其中a＞0，记的最大值为A。

（Ⅰ）求f＇（x）；

（Ⅱ）求A；

（Ⅲ）证明≤2A。

正确答案

见解析

解析

（Ⅰ）．

（Ⅱ）当时，

因此，． ………4分

当时，将变形为．

令，则是在上的最大值，，，且当时，取得极小值，极小值为．

令，解得（舍去），．

（ⅰ）当时，在内无极值点，，，，所以．

（ⅱ）当时，由，知．

又，所以．

综上，．　　　………9分

（Ⅲ）由（Ⅰ）得.

当时，.

当时，，所以.

知识点

复合函数的单调性

题型：填空题

填空题 · 4 分

13．设，，若对任意实数都有，则满足条件的有序实数组的组数为__________．

正确答案

解析

①当时，

若，则；若，则；

②当时，

若，则；若，则．

共组．

考查方向

三角函数性质，枚举法．

解题思路

根据三角函数的性质，枚举有序实数组的所有可能．

易错点

在枚举过程中漏考虑若干情形．

知识点

复合函数的单调性

题型：填空题

填空题 · 5 分

15.已知函数，，若，则实数m的取值范围是 .

正确答案

解析

由题可知，x<-1时，f(x)>f(-1)=e,则g(x)的最大值为-1，则m∈.

考查方向

本题主要考查了函数的图像性质

解题思路

本题考查函数的图像性质，解题思路如下：画出函数f(x)的图像及g(x)的图像；比较函数值的大小,并求出最大值。

易错点

本题必须注意单调性的比较

知识点

函数的定义域及其求法复合函数的单调性指数函数的图像与性质

继续学习学习下一知识点

下一知识点 : 函数的最值及其几何意义

百度题库 > 高考 > 理科数学 > 复合函数的单调性

扫码查看完整答案与解析