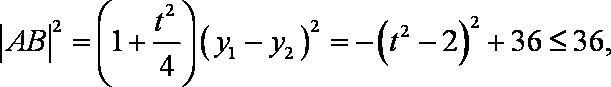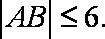- 复合函数的单调性
- 共394题
已知椭圆





(1)若
(2)对(1)中椭圆,求
(3)



正确答案
见解析
解析
(1)由已知,可得

∵


∴
(2)设


代入椭圆方程得




∴
(3)由已知椭圆方程为
右焦点

直线

由①②得:
设



设



∵点
∴
整理得:

又点


由③④⑤式得
知识点
已知抛物线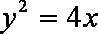

正确答案
6
解析
当直线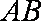
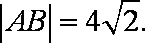
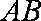
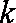
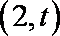
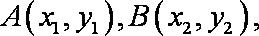
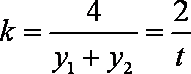
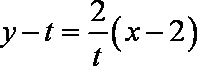
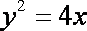
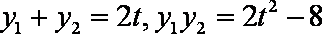
知识点
已知函数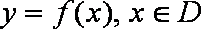
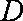
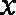

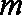
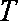
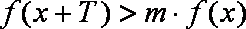
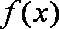
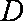
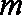
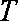
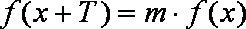
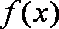
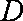
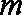
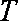
(1)已知函数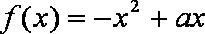
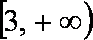
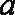
(2)已知 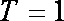
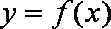
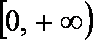
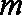
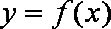
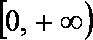
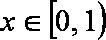
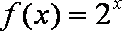
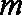
(3)下面两个问题可以任选一个问题作答,问题(Ⅰ)6分,问题(Ⅱ)8分,如果你选做了两个,我们将按照问题(Ⅰ)给你记分。
(Ⅰ)
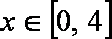
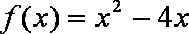
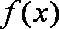

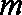
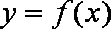
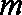
(Ⅱ)是否存在实数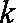
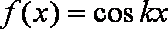
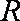
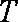
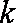
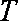
正确答案
见解析
解析
(1)由题意可知: 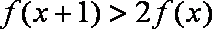
即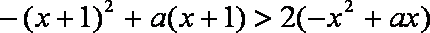
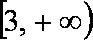

∵
∴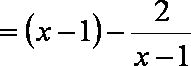
令
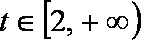
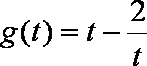
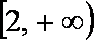
∴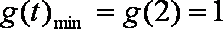
∴
(2
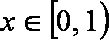
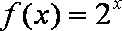
∴当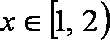
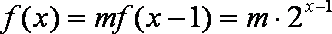
当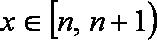
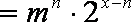
即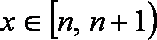
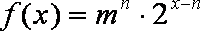
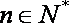
∵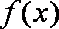
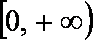
∴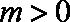
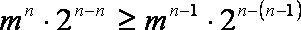
即
(3)问题(Ⅰ)∵当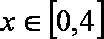
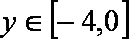
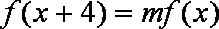
∴当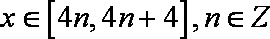
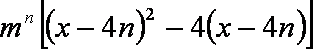
当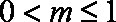
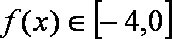
当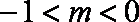

当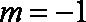
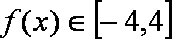
当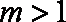
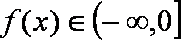
当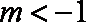
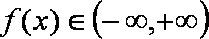
综上可知: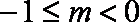
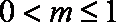
问题(Ⅱ):由已知,有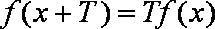
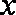
即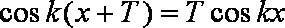
当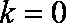
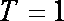
当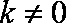
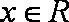
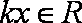
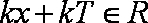
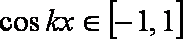
又∵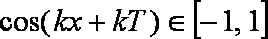
故要使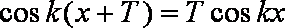
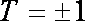

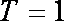
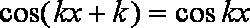
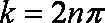
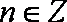
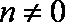
当
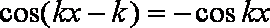
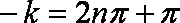
即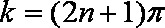
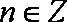
综上可知:当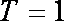
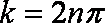
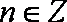
当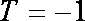
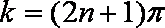
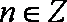
知识点
如图,两铁路线垂直相交于站







(1)求甲、乙两车的最近距离(用含
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为


正确答案
见解析
解析
(1)设两车距离为



即两车的最近距离是
(2)当两车相距最近时,
此时
即当车速


知识点
已知函数

正确答案
解析







知识点
扫码查看完整答案与解析