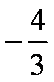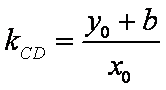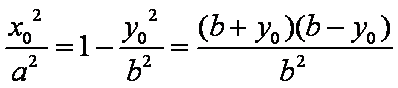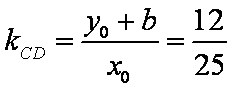- 复合函数的单调性
- 共394题
设函数

(1)求
(2)若




正确答案
(1)2(2)2
解析
解析:(1)由题意,对任意

即
即

因为

解法二:因为




当



所以

(2)由(1)


解得

故

令



所以
………………9分
当




解得
当




………………13分
综上,

………………14分
知识点
已知三个互不相等的正数









(1)若



(2)设





(3)若插入的






正确答案
(1)





解析
解析:(1)因为




由已知,





当插入的一个数位于






因为

(2)设所构成的等差数列的公差为


………………5分
若在





于是



若在





于是


若






解得
综上,




(3)设所构成的等差数列的公差为
由题意,



所以



所以,当





………………18分
知识点
已知函数

(1)求
(2)求
正确答案
见解析
解析
(1)令

所以

由 


由 


综上,函数


(2)
因为

当



当



知识点
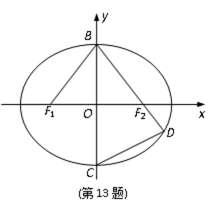
如图,在平面直角坐标系xOy中,F1,F2分别为椭圆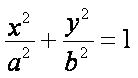
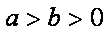
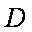
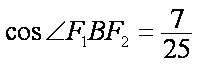
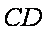
正确答案
解析
因为BF1=BF2=a,F1F2=2c,由余弦定理得
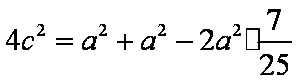
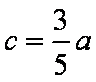
直线BF2的斜率为
设D(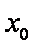
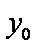
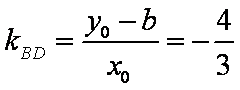
又D在椭圆上,故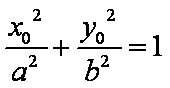
得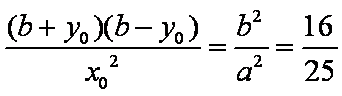
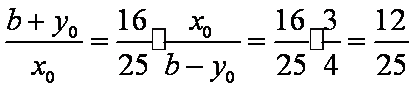
知识点
已知


正确答案
解析
因为

知识点
扫码查看完整答案与解析