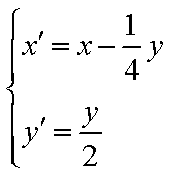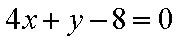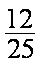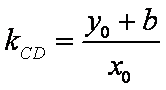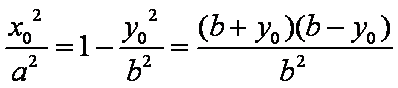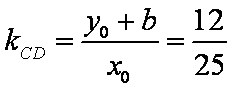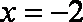- 复合函数的单调性
- 共394题
设函数

(1)求
(2)若




正确答案
(1)2(2)2
解析
解析:(1)由题意,对任意

即
即

因为

解法二:因为




当



所以

(2)由(1)


解得

故

令



所以
………………9分
当




解得
当




………………13分
综上,

………………14分
知识点
已知三个互不相等的正数









(1)若



(2)设





(3)若插入的






正确答案
(1)





解析
解析:(1)因为




由已知,





当插入的一个数位于






因为

(2)设所构成的等差数列的公差为


………………5分
若在





于是



若在





于是


若






解得
综上,




(3)设所构成的等差数列的公差为
由题意,



所以



所以,当





………………18分
知识点
已知函数

(1)求
(2)求
正确答案
见解析
解析
(1)令

所以

由 


由 


综上,函数


(2)
因为

当



当



知识点
已知矩阵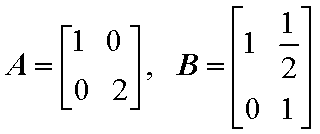
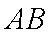
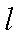
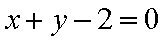
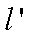
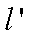
正确答案
见解析
解析
易得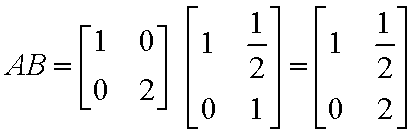
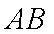
点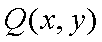
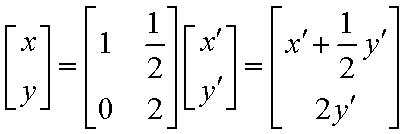
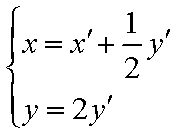
代入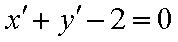
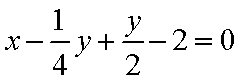
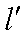
知识点
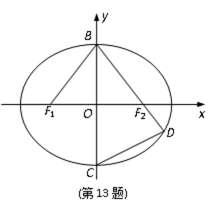
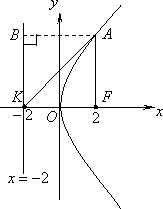
如图,在平面直角坐标系xOy中,F1,F2分别为椭圆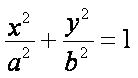
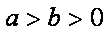
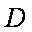
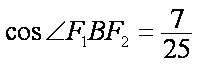
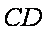
正确答案
解析
因为BF1=BF2=a,F1F2=2c,由余弦定理得
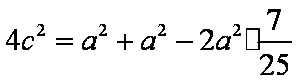
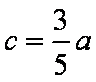
直线BF2的斜率为
设D(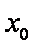
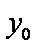
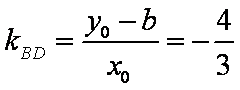
又D在椭圆上,故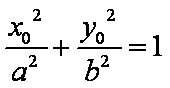
得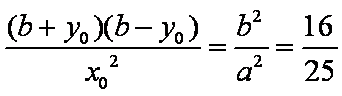
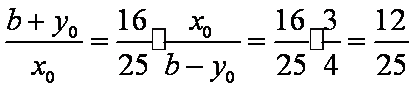
知识点
已知


正确答案
解析
因为

知识点
已知动点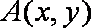
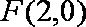
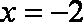
(1)求动点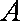
(2)记点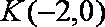

正确答案
(1)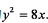
解析
解析:(1)由题意可知,动点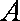

设方程为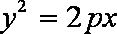

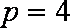
所以动点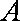
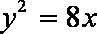
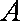
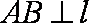
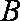
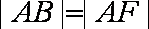
由于
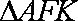
………2分

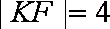
所以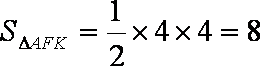
知识点
对于函数





(1)判断函数

(2)已知函数





正确答案
见解析
解析
(1)函数

因为由

(2) 由题意得,



而


① 当









②当









③ 当








则

综上所述,所求
知识点
如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成. 已知球的直径是

(1)这种“浮球”的体积是多少
(2)要在这样

正确答案
(1)169.9

解析
解析:(1)





(2)

1个“浮球”的表面积
2500个“浮球”的表面积的和
所用胶的质量为
答:这种浮球的体积约为

知识点
某车队准备从甲、乙等7辆车中选派4辆参加救援物资的运输工作,并按出发顺序前后排成一队,要求甲、乙至少有一辆参加,且若甲、乙同时参加,则它们出发时不能相邻,那么不同排法种数为
正确答案
解析
若甲乙只有一个参加,则有

知识点
扫码查看完整答案与解析