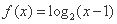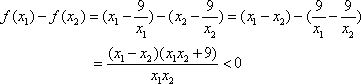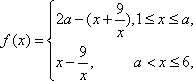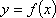- 复合函数的单调性
- 共394题
(本题满分14分)
已知函数
(1)设



(2)当


正确答案
见解析。
解析
(1)



即

于是

由



所以

因此,当






(2)解法一:当


故只需证明当


当


又
故



当



从而当


由


故



综上,当

解法二:当




取函数










所以


知识点
已知函数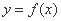
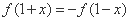
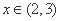
给出以下4个结论:
①函数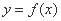
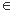
②函数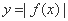
③当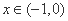

④函数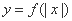
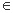
其一中所有正确结论的序号为
正确答案
①②③
解析
略
知识点
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张,为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列

(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
正确答案
(1)
解析
(1)
当


当



而
(2)当

当
由



知识点
已知函数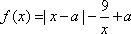
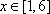
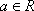
(1)若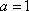
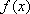
(2)当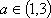
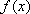
正确答案
见解析
解析
(1)判断:若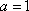
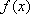
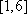
证明:当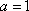
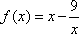
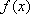
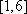
在区间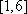
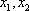
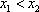
所以
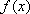
(2)因为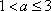
当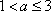
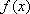
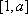
证明:当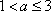
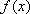
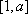
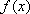
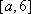
当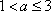
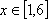
所以任意一个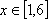
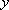
所以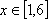
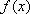
知识点



正确答案
解析
略
知识点
扫码查看完整答案与解析