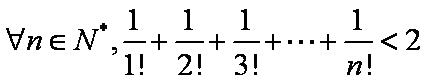- 复合函数的单调性
- 共394题
已知圆C的参数方程为
正确答案
见解析。
解析
圆C的参数方程为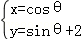
所以圆C的方程为 x2+(y﹣2)2=1;圆的圆心坐标(0,2),半径为1,
直线l的极坐标方程为ρsinθ+ρcosθ=1,
所以直线l的方程为 x+y=1。
圆心到直线的距离为:
圆心到直线的距离,半径,半弦长满足勾股定理,
故所求弦长为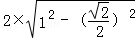
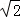
知识点
已知函数

(1)求
(2)设不等式



(3)设

正确答案
见解析
解析
(1)因为

令





所以函数


所以当


(2)因为不等式


所以对任意

由

当

将



当



所以


所以当


故实数

(3)由(1)知,对任意实数


令


所以
即
所以
因为
所以 
知识点
证明:
正确答案
见解析。
解析
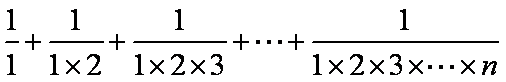

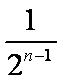
知识点
在直角坐标系中,曲线C的参数方程为



(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与直线C的两个交点为A、B,求
正确答案
见解析
解析
(1)直线
直线



(2)直线


将直线
有
设两根为

知识点
如图所示,四棱锥








(1)求证:平面

(2)求直线

(3)求点

正确答案
见解析
解析
解析:(1)设





则



又∵

又∵

∴
又∵




∵



(2)连结



则由(1)知平面

且
得





在

在


即直线


(3)由于








从而点


知识点
扫码查看完整答案与解析