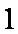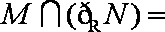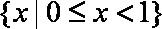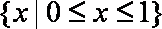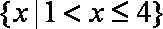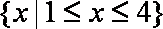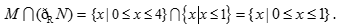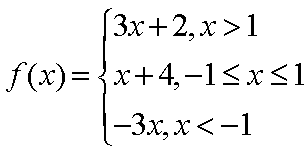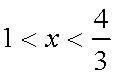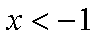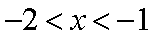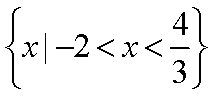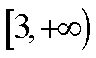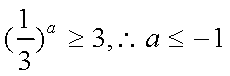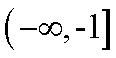- 集合与常用逻辑用语
- 共2295题
已知集合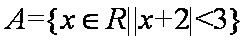
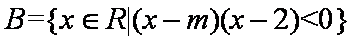
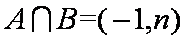
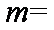
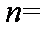
正确答案
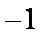
解析
∵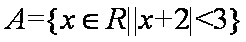
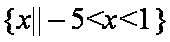
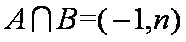
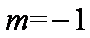
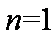
知识点
设数列
①
②所有项
③
设集合







(1)若数列

(2)设


(3)若数列







正确答案
见解析
解析
解析:
(1)1,4,7 ……………………3分
(2)由
当


当

当

当

∴
(3)∵
当
∴ 
由
因为使得


所以
当


当

所以
知识点
集合

正确答案
解析



知识点
已知集合



正确答案
解析




知识点
已知实数集R,集合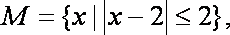
正确答案
解析
知识点
已知集合

正确答案
解析
知识点
已知全集




正确答案
解析


知识点
设全集


正确答案
解析



知识点
设集合A={


正确答案
解析
因为


知识点
已知函数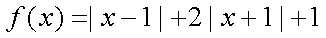
(1)求不等式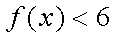
(2)若直线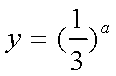
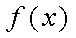

正确答案
见解析
解析
(1)因为
所以当
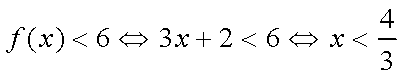

所以
当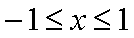
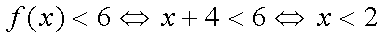
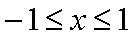
所以
当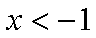
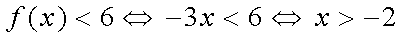
所以
综上,所求的解集为
(2)结合(1)可得,函数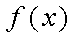
又直线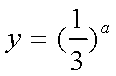
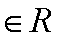
所以
即a的取值区间是
知识点
若全集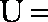
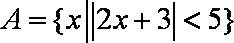
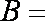
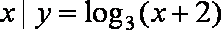
正确答案
解析
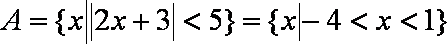
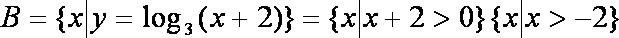
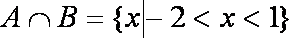
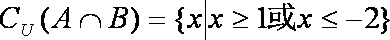
知识点
已知函数
(1)求
(2)设



正确答案
(1)单调递增区间为(0,-


(2)
解析
(1)
①当


②当




在区间(-


所以,当

当



(2)由已知,转化为

由(1)知,当

当



故f(x)的极大值即为最大值,
所以1>-1-ln(-a),解得:a<-
知识点
设集合A={x|x﹣a<1,x∈R},B={x|x﹣b>1,x∈R},若A⊆B,则实数a,b必满足( )
正确答案
解析
∵A={x|a﹣1<x<a+1},B={x|x<b﹣1或x>b+1}
因为A⊆B,所以a+1≤b﹣1或a﹣1≥b+1,即a﹣b≤﹣2或a﹣b≥2,即|a﹣b|≥2。故选A。
知识点
集合M={x|lgx>0},N={x|x2≤4},则M∩N=( )
正确答案
解析
∵M={x|lgx>0}={x|x>1},N={x|x2≤4}={x|﹣2≤x≤2},
∴ M∩N={x|1<x≤2},
故选C。
知识点
已知集合U={1,2,3,4,5,6},对于集合A⊆U,定义S(A)为A中所有元素之和,则全体S(A)的总和S= 。
正确答案
672
解析
∵ U={1,2,3,4,5,6},A⊆U,
则含1的满足条件的A共有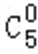
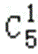
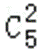
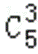
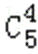
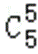
同理含2,3,4,5,6的满足条件的A也有32个
故S(A)=32×(1+2+3+4+5+6)=32×21=672
故答案为:672
知识点
扫码查看完整答案与解析