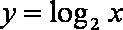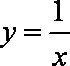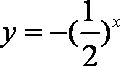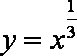- 集合与常用逻辑用语
- 共2295题
如图所示的几何体是由以等边三角形





(1) 求证:
(2) 求证:平面
(3) 求平面

正确答案
见解析
解析
证明:(1)取DE D中点G,建系如图,则A(0,
D(-1,0,1),E(1,0,3)、F(0,
=(2,0,2),=(1,
设平面DEF的一法向量
则

∴=(1,0,-1),平面ABC的一法




(2)显然,平面BCED的一法向量为=(0,1,0),

(3)由(1)知平面DEF的一法向量=(1,0,-1),平面ABC的一法向量=(0,0,1),
∴求平面


知识点
下列四个函数中,在区间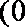
正确答案
解析
选项B是反比例函数,其图象在第一、三象限,故选B.
知识点
已知集合A=
若
正确答案
解析
解析:因为A=









知识点
执行如右图所示的程序框图,若输出的结果为

正确答案
解析
略
知识点
已知集合



正确答案
解析
略
知识点
已知集合


正确答案
解析
由




知识点
设集合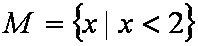
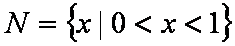
正确答案
解析
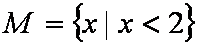
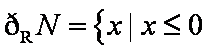
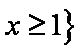
知识点
已知集合



①

③
其中是“垂直对点集”的序号是 。
正确答案
答案:
解析
略
知识点
定义
正确答案
见解析。
解析
当

当


当

所以
当





综上:
知识点
定义在R上的偶函数f(x﹣2),当x>﹣2时,f(x)=ex+1﹣2(e为自然对数的底数),若存在k∈Z,使方程f(x)=0的实数根x0∈(k﹣1,k),则k的取值集合是( )
正确答案
解析
∵ 偶函数f(x﹣2)的图关于y轴对称
∴ 函数y=f(x)的图象关于=﹣2对称
∵ 当x>﹣2时,f(x)=ex+1﹣2
∵ f(x)=ex+1﹣2在(﹣2,+∞)单调递增,且f(﹣1)<0,f(0)=e﹣2>0
由零点存在定理可知,函数f(x)=ex+1﹣2在(﹣1,0)上存在零点
由函数图象的对称性可知,当x<﹣2时,存在唯一零点x∈(﹣5,﹣4)
由题意方程f(x)=0的实数根x0∈(k﹣1,k),则k﹣1=﹣5或k﹣1=﹣1
k=﹣4或k=0
故选C
知识点
已知集合A={x∈R||x+2|<3},集合B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m= ,n=
正确答案
-1,1
解析
A={x∈R||x+2|<3}={x∈R|-5<x<1},
又集合B={x∈R|(x-m)(x-2)<0},A∩B=(-1,n)。
所以m=-1,n=1。
知识点
设函数

(1)求函数
(2)已知






(3)设



正确答案
见解析
解析
(1)
由


可知方程



当





则函数


(2)不妨设


令



故

当



(3)








令

由












因为




由


由


因为



令




所以



综上所述,实数a的取值范围是
知识点
已知集合

正确答案
解析
略
知识点
满足条件A∪{0,1,2}={0,1,2,3}的所有集合A的个数是
正确答案
解析
∵A∪{0,1,2}={0,1,2,3},
∴3∈A,
所以A可取:{3}; {0,3}、{1,3}、{2,3}、{0,1,3}、{0,2,3}、{1,2,3}、{0,1,2,3},一共8个,故选C
知识点
设集合A为函数y =ln(-x2-2x+8)的定义域,集合B为函数


(1) 求A∩B;
(2) 若
正确答案
见解析。
解析
(1)由-x2-2x+8>0,解得A=(-4,2),又
所以B=(-∞,-3]∪ [1,+∞),所以A∩B=(-4,-3]∪[1,2),
(2)因为∁RA=(-∞,-4]∪[2,+∞)。
由
① 当a>0时,由

② 当a<0时,由

欲使C⊆∁RA,则
解得-


综上所述,所求a的取值范围是
知识点
扫码查看完整答案与解析