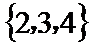- 集合与常用逻辑用语
- 共2295题
1.已知集合P=｛x∈R︱1≤x≤3｝，Q=｛x∈R︱x²≥4｝，则P∪（CRQ）= ( )
A[2,3]
B(-2,3]
C[1,2)
D
正确答案
解析
根据补集的运算得
考查方向
解题思路
先求集合
易错点
补集端点的取舍
知识点
11.已知集合
正确答案
{1,2,3}
解析
由题意得，
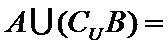
考查方向
解题思路
先求出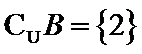
易错点
马虎出错。
知识点
1.已知全集
A
B
C
D
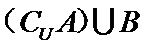
正确答案
解析
由题意得
考查方向
解题思路
1.先求出集合
2.利用集合的并集求出答案。
易错点
对于集合的交并补的符号不理解会导致错误。
知识点
1．设集合
A
B
C
D
正确答案
解析
因为
考查方向
解题思路
根据题意，先确定集合M和N表示的x的范围，然后在求交集和补集
易错点
集合的基本概念理解不透彻
知识点
7．设集合A={(x，y）|y≥|x-l|}，B={(x，y)|x-2y+2≥0），C={(x,y）|ax-y+a≥0}，
若(A
正确答案
解析
试题分析：本题属于线性规划中的基本问题，题目的难度是逐渐由易到难。注意动直线经过定点．
考查方向
本题主要考查了集合的基本运算和线性规划问题,在近几年的各省高考题出现的频率较高，常与不等式、函数、线性规划等知识点交汇命题。
解题思路
本题考查集合的基本运算和线性规划问题，解题步骤如下：
由题可知，画出A，B集合中的不等式所表示的阴影区域，C集合中的动直线经过定点（-1，0），利用图像易得斜率a≥1。
易错点
本题易在解不等式时发生错误。
知识点
1.已知全集 U=R，集合 A={x | y=log2 (-x2+x)}，B={ y | y=1+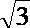
A{x | 0＜ x ＜1}
B{x | x＜ 0 }
C{x | x＞ 2 }
D{x |1＜x
正确答案
解析
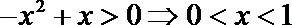
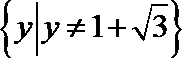
考查方向
本题主要考查了集合运算及函数性质
解题思路
先求出集合A的定义域，集合B的值域，然后在集合运算
易错点
1、对集合性质理解不透，集合A求定义域，集合B求值域
知识点
1．若全集U=R，集合
A
B
C
D
正确答案
解析
考查方向
解题思路
分别将A B集合化简过后求解即可
易错点
本题易在化简A集合时出错。
知识点
（4分）（2015•上海）设全集U=R．若集合Α={1，2，3，4}，Β={x|2≤x≤3}，则Α∩∁UΒ= ．
正确答案
{1,4}
知识点
若全集U=R，集合
A
B
C
D
正确答案
解析
考查方向
解题思路
分别将A B集合化简过后求解即可
易错点
本题易在化简A集合时出错。
知识点
1.设集合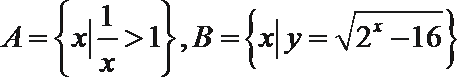
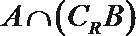
A
B
C
D
正确答案
解析
求解集合A的不等式得：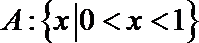
解集合B的不等式得：
所以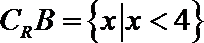
所以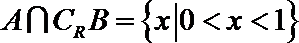
考查方向
本题主要考查集合间的基本关系，集合的交集和补集的概念和性质。常与不等式知识交汇命题。是基础题
解题思路
先解不等式，求出集合A和集合B，然后利用集合间的基本关系性质运算求解。
易错点
混淆交集、并集、补集的概念，不会解不等式
知识点
1．已知全集I＝R，集合A＝{x|y＝}，集合B＝{x|0≤x≤2}，则(∁IA)∪B等于( )
正确答案
解析
化简集合A={x|x
考查方向
解题思路
先化简集合A，然后求A 在I中的补集，最后求与B的并集.
易错点
化简集合A易出错，
知识点
1.已知集合P＝{
正确答案
解析
试题分析：由集合P＝{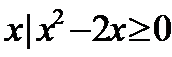
P＝{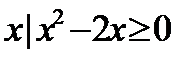
考查方向
解题思路
首先由集合P中的元素满足的不等式求出集合P，然后求出集合P的补集，
最后求出集合P的补集与集合Q的交集．
易错点
求集合P的过程中不要忘了等号.
知识点
1．已知集合A＝{x｜y＝
A（4，＋∞）
B[0，
C（
D（1，4]
正确答案
解析
考查方向
解题思路
本题属于简单题，可使用数轴表示出集合直接判断，
易错点
该题主要易错于对端点情况的判断错误
知识点
2.已知集合
A
B
C
D
正确答案
解析
由已知解出
因此A选项不正确，B选项不正确，D选项不正确，所以选C选项。
考查方向
解题思路
先解出集合B，再求出
易错点
对指数不等式的解法出错。
知识点
1.已知全集
A
B
C
D
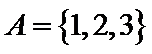
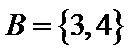
正确答案
解析
使用集合交集的性质，借助数轴容易得出答案C。
考查方向
解题思路
本题属于简单题，可使用venn图直接观察得出
易错点
直接观察漏解
知识点
扫码查看完整答案与解析