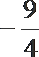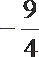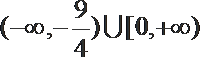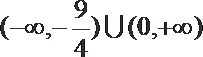- 集合与常用逻辑用语
- 共2295题
1.已知集合A={x|y=
正确答案
解析
考查方向
解题思路
本题属于简单题,可使用数轴表示出集合直接判断,
易错点
该题主要易错于对端点情况的判断错误
知识点
9.对于集合M、N,定义M-N={x|x∈M且x∉N},M⊕N=(M-N)∪(N-M),设A={y|y=3x, x∈R},B={y|y=-(x-1)2+2,x∈R},则A⊕B等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给定集合


正确答案
5 ;2m - 3
解析
解析已在路上飞奔,马上就到!
知识点
14.已知全集为





① 对任意

②对任意


③对任意

④对任意

其中,正确结论的序号是__________。
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
12.已知集合M={



①M={
②M={
③M={
④M={
其中是“垂直对点集”的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设集合




正确答案
解析










(4,3)共8组,若

知识点
设
正确答案
解析
本题考查了集合的运算、不等式的解法
Q=(-2,2),故Q
知识点
13.非空集合G关于运算⊕满足:
(1)对任意的a,b∈G,都有a⊕b∈G,
(2)存在e∈G,都有a⊕e=e⊕a=a,则称G关于运算⊕为“融洽集”.
现给出下列集合和运算:
①G={非负整数},⊕为整数的加法.
②G={偶数},⊕为整数的乘法.
③G={平面向量},⊕为平面向量的加法.
④G={二次三项式},⊕为多项式的加法.
⑤G={虚数},⊕为复数的乘法.
其中G关于运算⊕为“融洽集”的是__________.(写出所有“融洽集”的序号)
正确答案
①③
解析
①G={非负整数},⊕为整数的加法,满足任意a,b∈G,都有a⊕b∈G,且令e=0,有a⊕0=0⊕a=a
∴①符合要求;
②G={偶数},⊕为整数的乘法,若存在a⊕e=a×e=a,则e=1,矛盾
∴②不符合要求;
③G={平面向量},⊕为平面向量的加法,两个向量相加结果仍为向量;取
∴③符合要求;
④G={二次三项式},⊕为多项式的加法,两个二次三项式相加得到的可能不是二次三项式
∴④不符合要求;
⑤G={虚数},⊕为复数的乘法,两个虚数相乘得到的可能是实数
∴⑤不符合要求,
这样G关于运算⊕为“融洽集”的有①③.故答案为:①③.
知识点
14.设集合







① 
② 
⑤ 
④ 整数集
以0为聚点的集合有__________ .(请写出所有满足条件的集合的编号)
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
已知集合


正确答案
解析
略
知识点
6.设A,B是有限集,定义d(A,B)=card(A,B)=card(A∪B)-card(A∩B),其中card(A)表示有限集A中的元素个数,
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C),
正确答案
解析
试题分析:根据充分性和必要性判断出命题①正确;根据集合间的关系判断出命
题②正确。
命题①:对任意有限集A,B,若“A≠B”,则A∪B≠A∩B,则card(A∪B)>car(A∩B),
故“d(A,B)>0”成立,
若d(A,B)>0”,则card(A∪B)>card(A∩B),则A∪B≠A∩B,故A≠B成立,故
命题①成立,
命题②,d(A,B)=card(A∪B)-card(A∩B),d(B,C)=card(B∪C)-card
(B∩C),
∴d(A,B)+d(B,C)=card(A∪B)-card(A∩B)+card(B∪C)-card(B∩C)=[card
(A∪B)+card(B∪C)]-[card(A∩B)+card(B∩C)]
≥card(A∪C)-card(A∩C)=d(A,C),故命题②成立,
故选:A:
考查方向
解题思路
根据充分必要条件的条件进行判断命题①;借助新定义和集合的运算判断命
题②,从而得出结论.
易错点
充分必要条件要从充分性和必要性两个方面来证明.
知识点
10.对于集合M、N,定义: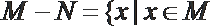
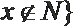
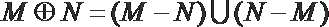
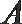
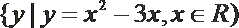
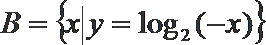

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于集合N={1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对n=3、n=4的情况,计算它的“交替和”的总和S3、S4,并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和Sn= _______。
正确答案
n∙2n–1
解析
解析已在路上飞奔,马上就到!
知识点
命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
正确答案
解析
本题主要考查否命题的概念 ,属于容易题。
否命题是同时否定命题的条件结论,故否命题的定义可知B项是正确的。
【温馨提示】解题时要注意否命题与命题否定的区别。
知识点
9.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析