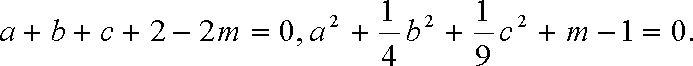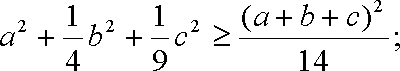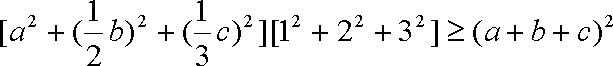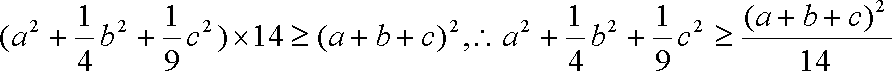- 集合与常用逻辑用语
- 共2295题
已知


(1)令








(2)若函数



正确答案
见解析
解析
(1)
由题意,不妨设


∴


∵
∴

(2)


要使



令
∵



∴
由上知
∴

令

∴


∴ 
故

知识点
已知集合A={x∈R||x|≥2},B={x∈R|x2﹣x﹣2<0}且R为实数集,则下列结论正确的是( )
正确答案
解析
集合A={x∈R||x|≥2}={x∈R|x≥2或x≤﹣2},B={x∈R|x2﹣x﹣2<0}={x∈R|﹣1<x<2}。
所以A∪B={x∈R|x>﹣1或x≤﹣2},所以A错误。
所以A∩B=∅,所以B错误。
∁RB={x∈R|x≥2或x≤﹣1},所以A⊆(∁RB),所以C正确,D错误。
知识点
设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则A∩∁UB=()
正确答案
解析
解:∵全集U={1,2,3,4,5},集合A={1,2},B={2,3},
∴∁UB={1,4,5}
A∩∁UB={1,2}∩{1,4,5}={1}
故选C。
知识点
已知集合



正确答案
解析
易知A={-1,0,1},B={1,2},故A∩B={1}.
知识点
用1,2,3,4这四个数字组成无重复数字的四位数,其中恰有一个偶数字夹在两个奇数字之间的四位数的个数为
正确答案
8种
解析
知识点
已知集合


正确答案
解析



知识点
设变量x,y满足约束条件
正确答案
解析
画出可行域,如图所示,将目标函数变形为





知识点
已知
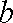

(1)求证:
(2)若求实数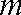
正确答案
见解析
解析
(1)由柯西不等式得
即
当且仅当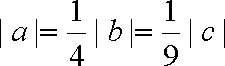
(2)由已知得
又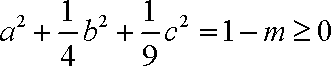
∴
∴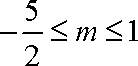
知识点
设集合M={-1,0,1},N={x | x2 ≤ x},则M∩N =( )
正确答案
解析


知识点
已知集合


正确答案
解析
由已知得,直线







知识点
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A、B、C,其中







对于“完并集合”
正确答案
3
解析
因为









知识点
如图,












(1)求证:直线

(2)直线





正确答案
见解析 。
解析
(1)证明:





又


(2)解:以







则



则






依题意得

知识点
选修4-5:不等式选讲
已知集合
(1)求A的解集;
(2)若

正确答案
见解析。
解析
(1)由不等式几何意义可知
(2) 
知识点
已知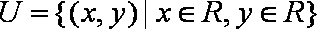
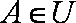
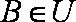
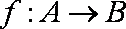
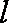
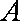
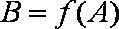
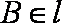
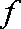
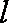
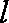
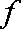
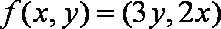
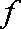
正确答案
解析
设直线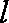
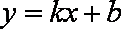
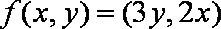
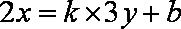
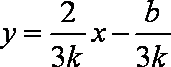
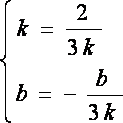
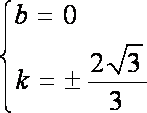
知识点
如图,在





(1)边
(2)

正确答案
见解析。
解析
(1)由


由正弦定理 

(2)
由余弦定理:
知识点
扫码查看完整答案与解析