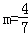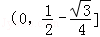- 集合与常用逻辑用语
- 共2295题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
复数
正确答案
解析
略
知识点
已知数列{an}满足a1=1,an+1=3an+1.
正确答案
见解析。
解析
知识点
如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上)。
求证:AB∶AC为定值。
正确答案
见解析
解析
证明:连结AO1,并延长分别交两圆于点E和点D.连结BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上.故AD,AE分别为圆O1,圆O2的直径。
从而∠ABD=∠ACE=
于是
所以AB∶AC为定值。
知识点
如图6,四棱锥







(1)求证:
(2)


是否存在实数


若存在,求
正确答案
见解析。
解析
(1)连接
(方法一)





因为
(方法二)



因为

因为

(2)(方法一)过




连接


又


依题意,





在


所以


(方法二)在平面









则


设

解得

由(1)知


所以
解得
(方法三)过








由(1)及余弦定理得
所以


知识点
已知集合


正确答案
解析
略
知识点
在数列



(1)求
(2)若对一切

正确答案
见解析。
解析
知识点
已知全集U={0,1,2,3,4},集合A={0,1,2,3},B={2,3,4},那么CU(A∩B)( )
正确答案
解析
∵ 集合A={0,1,2,3},B={2,3,4},
∴ A∩B={2,3},
又全集U={0,1,2,3,4},则CU(A∩B)={O,1,4},故选:C。
知识点
已知正六边形ABCDEF的边长是2,一条抛物线恰好经过该六边形的四个顶点,则抛物线的焦点到准线的距离是( )
正确答案
解析
由题意,设正六边形ABCDEF的顶点A、B、C、F在抛物线y2=2px上,
设A(x1,1),F(x2,2),可得
由②、③消去p得x2=4x1,代入①可得x
所以x1=

根据抛物线的性质,可得焦点到准线的距离是p=
知识点
已知M,N为集合I的非空真子集,且M,N不相等,若N∩C1M=∅,则M∪N=( )
正确答案
解析
利用韦恩图画出满足题意的集合。
由图可得:M∪N=M。
故选A。
知识点
设集合A={


正确答案
解析
略
知识点
已知正数a,b,c满足a+b=ab,a+b+c=abc,则c的取值范围是 。
正确答案
解析
∵ 正数a,b,c满足a+b=ab,∴ 

∴ 
∵ a+b+c=abc,∴ab+c=abc,∴ c=

∵ ab≥4,∴ 

∴ c的取值范围是
知识点
已知集合Sn={(x1,x2,…,xn)|x1,x2,…,xn是正整数1,2,3,…,n的一个排列}(n≥2),函数
对于(a1,a2,…an)∈Sn,定义:bi=g(ai﹣a1)+g(ai﹣a2)+…+g(ai﹣ai﹣1),i∈{2,3,…,n},b1=0,称bi为ai的满意指数,排列b1,b2,…,bn为排列a1,a2,…,an的生成列;排列a1,a2,…,an为排列b1,b2,…,bn的母列。
(1)当n=6时,写出排列3,5,1,4,6,2的生成列及排列0,﹣1,2,﹣3,4,3的母列;
(2)证明:若a1,a2,…,an和a′1,a′2,…,a′n为Sn中两个不同排列,则它们的生成列也不同;
(3)对于Sn中的排列a1,a2,…,an,定义变换τ:将排列a1,a2,…,an从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列,证明:一定可以经过有限次变换τ将排列a1,a2,…,an变换为各项满意指数均为非负数的排列。
正确答案
见解析
解析
(1)解:当n=6时,排列3,5,1,4,6,2的生成列为0,1,﹣2,1,4,﹣3;
排列0,﹣1,2,﹣3,4,3的母列为3,2,4,1,6,5。
(2)证明:设a1,a2,…,an的生成列是b1,b2,…,bn;a′1,a′2,…,a′n的生成列是与b′1,b′2,…,b′n,
从右往左数,设排列a1,a2,…,an与a′1,a′2,…,a′n第一个不同的项为ak与a′k,即:an=a′n,an﹣1=a′n﹣1,…,ak+1=a′k+1,ak≠a′k。
显然 bn=b′n,bn﹣1=b′n﹣1,…,bk+1=b′k+1,下面证明:bk≠b′k。
由满意指数的定义知,ai的满意指数为排列a1,a2,…,an中前i﹣1项中比ai小的项的个数减去比ai大的项的个数。
由于排列a1,a2,…,an的前k项各不相同,设这k项中有l项比ak小,则有k﹣l﹣1项比ak大,从而bk=l﹣(k﹣l﹣1)=2l﹣k+1。
同理,设排列a′1,a′2,…,a′n中有l′项比a′k小,则有k﹣l′﹣1项比a′k大,从而b′k=2l′﹣k+1。
因为 a1,a2,…,ak与a′1,a′2,…,a′k是k个不同数的两个不同排列,且ak≠a′k,
所以 l≠l′,从而 bk≠b′k。
所以排列a1,a2,…,an和a′1,a′2,…,a′n的生成列也不同。
(3)证明:设排列a1,a2,…,an的生成列为b1,b2,…,bn,且ak为a1,a2,…,an中从左至右第一个满意指数为负数的项,所以 b1≥0,b2≥0,…,bk﹣1≥0,bk≤﹣1。
进行一次变换τ后,排列a1,a2,…,an变换为ak,a1,a2,…ak﹣1,ak+1,…,an,设该排列的生成列为b′1,b′2,…,b′n。
所以 (b′1,b′2,…,b′n)﹣(b1+b2+…+bn)=[g(a1﹣ak)+g(a2﹣ak)+…+g(ak﹣1﹣ak)]﹣[g(ak﹣a1)+g(ak﹣a2)+…+g(ak﹣ak﹣1)]=﹣2[g(ak﹣a1)+g(ak﹣a2)+…+g(ak﹣ak﹣1)]=﹣2bk≥2。
因此,经过一次变换τ后,整个排列的各项满意指数之和将至少增加2。
因为ai的满意指数bi≤i﹣1,其中i=1,2,3,…,n,
所以,整个排列的各项满意指数之和不超过1+2+3+…+(n﹣1)=
即整个排列的各项满意指数之和为有限数,
所以经过有限次变换τ后,一定会使各项的满意指数均为非负数。
知识点
集合


正确答案
解析
略
知识点
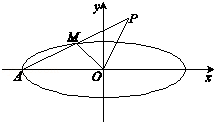
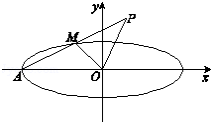
如图,椭圆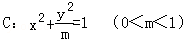
(1)若点P的坐标为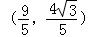
(2)若椭圆C上存在点M,使得OP⊥OM,求m的取值范围。
正确答案
(1)
(2)
解析
(1)依题意,M是线段AP的中点,
因为A(﹣1,0),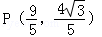
所以 点M的坐标为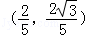
由于点M在椭圆C上,
所以 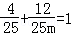
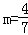
(2)设M(x0,y0)(﹣1<x0<1),则 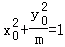
因为 M是线段AP的中点,所以 P(2x0+1,2y0)。
因为 OP⊥OM,所以
所以
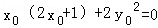
由 ①,②消去y0,整理得 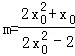
所以 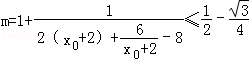
当且仅当 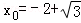
所以m的取值范围是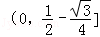
知识点
扫码查看完整答案与解析