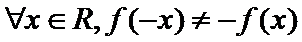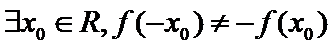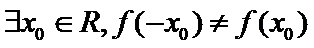- 集合与常用逻辑用语
- 共2295题
设p:实数x,y满足(x–1)2–(y–1)2≤2,q:实数x,y满足
正确答案
知识点
4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为150C,B点表示四月的平均最低气温约为50C。下面叙述不正确的是
正确答案
知识点
5.设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,
正确答案
解析
由题意得,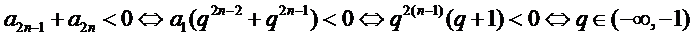
考查方向
解题思路
充分、必要条件的判断可以用定义法、等价法货集合法.本题直接利用数列的通项公式进行转化即可解决。
易错点
不能灵活应用数列的通项公式已知条件进行转化导致出错。
知识点
α、β是两个平面,m、n是两条直线,有下列四个命题:
①如果m⊥n,m⊥α,n∥β,那么α⊥β.
②如果m⊥α,n∥α,那么m⊥n.
③如果α∥β,m
④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有 .(填写所有正确命题的编号)
正确答案
②③④
知识点
在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为
当P是原点时,定义P的“伴随点“为它自身,平面曲线C上所有点的“伴随点”所构成的曲线
①若点A的“伴随点”是点

②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序列).
正确答案
知识点
4.设a,b是向量,则“







正确答案
知识点
15.设


正确答案
解析
设


由子集与推出关系可知“

考查方向
解题思路
利用子集与推出关系求解.
易错点
子集与推出关系.
知识点
7.若




正确答案
解析
若










考查方向
解题思路
利用直线与平面平行于垂直的关系,结合充分条件和必要条件性质,判断关系。
易错点
逻辑混乱,直线与平面的位置关系掌握不牢
知识点
4.设


正确答案
解析




考查方向
解题思路
直接按充分条件与必要条件的方法去判断。
易错点
判断失误。
知识点
3.设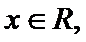
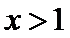
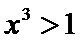
正确答案
解析
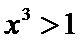
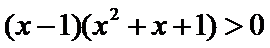
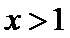
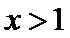
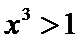
考查方向
解题思路
先解不等式得到前后范围相同,后即可得到答案。
易错点
不会解不等式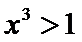
知识点
3.下列选项错误的是()
正确答案
解析
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全(特)称命题的否定确定C正确
4、最后选择D
考查方向
解题思路
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全(特)称命题的否定确定C正确
4、最后选择D
易错点
本题易错于全(特)称命题的否定理解不足,导致无法排除
知识点
5.已知命题







正确答案
解析




考查方向
解题思路
分别判断命题p,q的真假, 再分析复合命题的真假
易错点
复合命题的真值判断易出错
知识点
2.若直线



正确答案
解析
由向量共线的定义可知,两直线平行可以得到
考查方向
解题思路
分别判断。
易错点
判断出错。
知识点
13.若



正确答案
解析
由判别式小于等于0,即实数

考查方向
解题思路
直接由判别式小于等于0即可。
易错点
不会转化。
知识点
3.设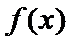
正确答案
考查方向
解题思路
1.先根据奇函数的定义得到题中命题的逆否命题;
易错点
1.全称命题的否定形式写错;2.不能正确理解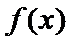
知识点
扫码查看完整答案与解析