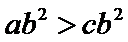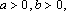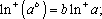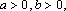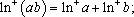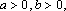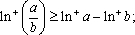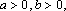- 集合与常用逻辑用语
- 共2295题
设{an}是首项为正数的等比数列，公比为q，则“q<0”是“对任意的正整数n，a2n−1+a2n<0”的
正确答案
知识点
15．设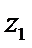
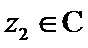
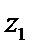
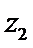
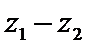
正确答案
解析
若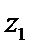
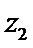
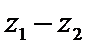
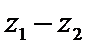
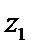
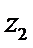
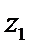
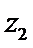
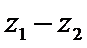
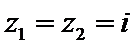
考查方向
解题思路
形如a＋bi(a，b∈R)的数叫复数，其中a，b分别是它的实部和虚部．若b＝0，则a＋bi为实数；若b≠0，则a＋bi为虚数；若a＝0且b≠0，则a＋bi为纯虚数．判断概念必须从其定义出发，不可想当然.
易错点
复数相等的条件
知识点
4. 下列叙述中正确的是（ ）
A若
B若
C命题“对任意
D
正确答案
解析
A.不正确，a<0不成立；B.不正确，如b=0; C不正确，命题“对任意
考查方向
解题思路
按照题中涉及到相关知识点，运用命题的知识点逐一排查。
易错点
不理解条件与结论之间的关系导致出错。全称命题的否定不理解。
知识点
3.命题“
A
B
C
D
正确答案
解析
由于全称命题的否定为特称命题，
故“
故选D.
考查方向
解题思路
根据全称命题的否定是特称命题进行转化格式即可.
易错点
否定形式为：改量词，否结论.
知识点
2．命题“
A
B
C
D
正确答案
解析
因为特称命题的否定是全称命题，所以，命题“∃a∈[0，+∞），sina＞a”的否定形式是∀a∈[0，+∞），sina≤a，故选：A．
考查方向
命题的否定
解题思路
利用特称命题的否定是全称命题写出结果即可
易错点
逻辑思维混乱
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
下列命题中，假命题为( )
A存在四边相等的四边形不是正方形
Bz1，z2∈
C若x，y∈
D对于任意n∈
正确答案
解析
A项中，四边相等的空间四边形显然不是正方形，故A项为真命题；B项中，z1，z2∈C，“z1＋z2为实数”⇐“z1，z2互为共轭复数”，但“z1＋z2为实数”D
知识点
如图，正方体ABCD－A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S.则下列命题正确的是__________（写出所有正确命题的编号）。
①当0＜CQ＜
②当CQ＝
③当CQ＝
④当
⑤当CQ＝1时，S的面积为
正确答案
①②③⑤
解析
如图（2），当CQ＝
图（2）
如图（3）所示，当
当CQ＝1时，截面为APC1E，
图（3）
可知AC1＝
知识点
定义“正对数”: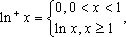 
①若
②若
③若
④若
其中真命题有____________.（写出所有真命题的编号）
正确答案
①③④
解析
略。
知识点
在空间，下列命题正确的是（ ）
正确答案
解析
由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案。
知识点
设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和，则下列命题错误的是
A若d＜0，则数列{S n}有最大项
B若数列{S n}有最大项，则d＜0
C若数列{S n}是递增数列，则对任意的n
D若对任意的n
正确答案
解析
选项C显然是错的，举出反例：—1，0，1，2，3，…，满足数列{S n}是递增数列，但是S n＞0不成立。
知识点
给出下列四个命题，其中假命题是（ ）
A从匀速传递的新产品生产流水线上，质检员每10分钟从中抽取一件新产品进行某项指标检测，这样的抽样是分层抽样；
B样本方差反映了样本数据与样本平均值的偏离程度；
C在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
D设随机变量
正确答案
解析
.选项A中的抽样为系统抽样，故此命题为假命题.其它选项为真命题.故选A
知识点
在下列命题 ①
正确答案
解析
略
知识点
若数列{an}的前n项和为Sn，则下列命题正确的是（ ）
正确答案
解析
解：A：数列{an}的前n项和为Sn，故 Sn =a1+a2+a3+…+an，
若数列{an}是递增数列，则数列{Sn}不一定是递增数列，如an=n﹣60，当an＜0 时，数列{Sn}是递减数列，故A不正确。
B：由数列{Sn}是递增数列，不能推出数列{an}的各项均为正数，
如数列：0，1，2，3，…，满足{Sn}是递增数列，但不满足数列{an}的各项均为正数，故B不正确。
C：若{an}是等差数列（公差d≠0），则由S1•S2…Sk=0不能推出a1•a2…ak=0，
例如数列：﹣3，﹣1，1，3，满足S4=0，但 a1•a2•a3•a4≠0，故C不正确。
D：一方面：若{an}是等比数列，则由S1•S2…Sk=0（k≥2，k∈N），
从而当k=2时，有S1•S2=0⇒S2=0⇒a1+a2=0，
∴a2=﹣a1，从而数列的{an}公比为﹣1，故有ak+ak+1=ak﹣ak=0。
另一方面，由ak+ak+1=0可得ak=﹣ak+1，∴a2=﹣a1，
可得S2=0，∴S1•S2…Sk=0（k≥2，k∈N），故D正确。
故选D。
知识点
下列关于不等式的说法正确的是( )
A任意实数a,b，都有
B任意实数x，
C不等式
D不等式
正确答案
解析
根据基本不等式成立的条件是“一正二定三相等”可知A不正确，因为a、b不一定是正实数；C中一元二次方程的根是1+a和1-a，但是当
知识点
扫码查看完整答案与解析