集合与常用逻辑用语_章节学习

1

题型：填空题

|

填空题 · 5 分

11.若“，”为真命题，则实数的最大值为 .

正确答案

0

解析

根据函数性质上的最小值为

∴

考查方向

本题主要考察了正切函数的性质，考察了函数的恒成立问题，难度系数不高，

解题思路

1、求出的最小值2、根据题意得出

易错点

本题易错在恒成立问题的转化

知识点

命题的真假判断与应用

1

题型：填空题

|

填空题 · 5 分

15．设S为复数集C的非空子集．如果

（1）S含有一个不等于0的数；

（2）∀a，b∈S，a+b，a﹣b，ab∈S；

（3）∀a，b∈S，且b≠0，∈S，那么就称S是一个数域．

现有如下命题：

①如果S是一个数域，则0，1∈S；

②如果S是一个数域，那么S含有无限多个数；

③复数集是数域；

④是数域；

⑤S={a+bi|a，b∈Z}是数域．

其中是真命题的有　　　　　　（写出所有真命题的序号）．

正确答案

①②③④

解析

由已知中（1）S含有一个不等于0的数；

（2）∀a，b∈S，a+b，a﹣b，ab∈S；

（3）∀a，b∈S，且b≠0，∈S，那么就称S是一个数域．

令a=b≠0，

则a﹣b=0∈S； =1∈S，故①正确；

na∈S，n∈Z，故②正确；

复数集C满足3个条件，故复数集是数域，故③正确；

满足3个条件，故S是数域，故④正确；

S={a+bi|a，b∈Z}不满足条件（3），故S不是数域，故⑤错误；

故答案为：①②③④

考查方向

本题主要以命题的真假判断与应用为载体考查了元素与集合关系的判断及复数的基本概念等知识，考查考生分析问题解决问题的能力，逻辑推理的能力，由于涉及到数域这个新概念，较难。

解题思路

根据已知中数域的概念，逐一分析5个命题的真假，综合讨论结果，可得答案。

易错点

1、本题由于未能正确理解数域的概念而导致判断出错。2、本题由于对此集合的理解不到位从而导致判断出错。

知识点

命题的真假判断与应用

1

题型：单选题

|

单选题 · 5 分

17．对于两个平面和两条直线，下列命题中真命题是（）

A若，，则

B若，，则

C若，，，则

D若，，，则

正确答案

D

解析

选项A：符合题设条件的直线也可能在平面上，如下右图所示，故选项A错；

选项B：符合题设条件的直线可能垂直于在平面，可能在平面上，可能平行于平面，也可能与平面斜交，故选项B错；

选项C：由图可知直线与直线可能平行，也可能成相交，也可能异面，所成的角的取值范围为，故选项C错误；从而可得选项D正确．

考查方向

本题考查了空间直线与平面的位置关系，考查了空间想象能力，是容易题．

解题思路

假命题举反例即可．

易错点

符合条件的空间直线和平面的位置关系有时候并不是只有结论的这一种，空间想象能力弱的话有时候未必能想得到．

知识点

命题的真假判断与应用空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系

1

题型：单选题

|

单选题 · 5 分

若是异面直线，则下列命题中的假命题为（　　）

A过直线可以作一个平面并且只可以作一个平面与直线平行；

B过直线至多可以作一个平面与直线垂直；

C唯一存在一个平面与直线等距；

D可能存在平面与直线都垂直。

正确答案

D

解析

能存在平面与直线都垂直是错误的，

因为平面与直线都垂直，

则直线平行，与直线是异面是矛盾的。

考查方向

本题主要考查异面直线的概念以及空间想象力，是常考题型

易错点

对空间想象力要求较高，需要一定的基础

知识点

命题的真假判断与应用异面直线及其所成的角空间中直线与直线之间的位置关系

1

题型：单选题

|

单选题 · 5 分

12．关于函数，下列说法错误的是

A是的极小值点

B函数有且只有1个零点

C存在正实数，使得恒成立

D对任意两个正实数，且，若，则

正确答案

C

解析

，，

且当时，，函数递减，

当时，，函数递增，

因此是的极小值点，A正确；

，

所以当时，恒成立，即单调递减，

又，，

所以有零点且只有一个零点，B正确；

设，

易知当时，，

对任意的正实数，

显然当时，，即，，

所以不成立，C错误；

作为选择题这时可得结论，选C，

下面对D研究，因为，

即，变形为，

设，，代入上式解得，所以，由导数的知识可证明是增函数，

又（洛必达法则），

所以，即命题的判断

考查方向

函数的性质，知识点多，难度大。

解题思路

根据函数的性质，依次判断每个选项

易错点

对命题理解不透彻，对函数的性质掌握不好

知识点

命题的真假判断与应用导数的运算

1

题型：简答题

|

简答题 · 5 分

14.以下四个命题中：

①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样,

②两个随机变量的线性相关性越强，相关系数的绝对值越接近于1,

③某项测量结果服从正态分布N (1，a2),P(≤5)=0.81，则P ≤ 3) =0.19

④对于两个分类变量X与Y的随机变量K2的观测值k来说，k越小，判断“X与Y有关系” 的把握程度越大。以上命题中其中真命题的个数为 .

正确答案

2

解析

（1）是系统抽样，所以（1）为假命题；

（2）根据|r|越趋近于1，两个随机变量的相关性越强，得（2）是真命题；

（3）根据正态分布的对称性，得（3）是真命题；

(4)根据两个分类变量X与Y的随机变量的观测值K来说，k越大，判断“X与Y有关系” 的把握程度越大。得（4）是假命题；所以命题中其中真命题的个数为2

考查方向

本题主要考查了统计基础知识和变量的相关性及离散性随机变量、正态分布

解题思路

利用系统抽样方法的特征判断命题1；根据|r|越趋近于

1，两个随机变量的相关性判断命题

2；利用正态分布的对称性判断命题

3；利用随机变量的观测值判断命题4

易错点

基础知识混淆，概念掌握不清

知识点

命题的真假判断与应用

1

题型：单选题

|

单选题 · 5 分

15．下列四个命题中，为真命题的是（）

A若，则

B若，，则

C若，则

D若，则

正确答案

C

解析

选项A：当时，若，则，故选项A错；

选项B：当时，满足条件，，但，故选项B错；

选项C：若，而，由不等式的传递性可得两边平方，可得，所以，故选项C正确；

选项D：当时，满足条件，但，故选项D错．

考查方向

本题主要考查不等式的基本性质，属于容易题，在近几年的各省高考题中出现的频率较高．

解题思路

对照不等式的八个基本性质，逐项判断每个选项的真假，错误的选项举出反例即可．

易错点

不等式的八个基本性质中每个性质需要的前提条件容易混淆．

知识点

命题的真假判断与应用不等式的性质

1

题型：单选题

|

单选题 · 5 分

12.函数.给出函数下列性质：

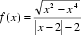
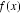
①函数的定义域和值域均为；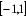

②函数的图像关于原点成中心对称；

③函数在定义域上单调递增；

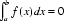
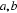
④（其中为函数在定义域上的积分下限和上限）；

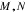
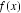
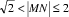
⑤为函数图象上任意不同两点，则.

则关于函数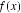性质正确描述的序号为（）

A①②⑤

B①③⑤

C②③④

D②④

正确答案

D

解析

根据已知解析式可知，

函数，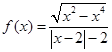

因为-1 ，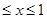

那么原式化简为，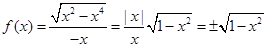

然后分析函数的定义域和值域均为，错误。

函数是奇函数，可知关于原点成中心对称，

同时在定义域内递增，并且命题4，利用对称性可知定积分值为零，

命题5中，不成立，故正确的序号为②④。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查函数的性质

解题思路

1、化简函数解析式；

2、依次判断每个命题，即可得到结果。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

易错点

本题易在判断化简时发生错误。

知识点

命题的真假判断与应用函数的定义域及其求法函数的值域奇偶函数图象的对称性

1

题型：单选题

|

单选题 · 5 分

4．设a，l是直线，α和β是平面，则下列说法正确的是（）

A若α⊥β，l∥α，则l⊥β

B若α⊥β，l⊥a，则l∥β

C若l∥α，l∥β，则α∥β

D若l∥α，l⊥β，则α⊥β

正确答案

D

解析

试题分析：本题属于立体几何中的基本问题，题目的难度是简单。

考查方向

本题主要考查了线面位置关系,在近几年的各省高考题出现的频率较高。

解题思路

本题考查线面位置关系，解题步骤如下：

由题可知，A中可能l∥β；B中可能l在β内；C中可能α⊥β。

易错点

本题易在判断线是否在面上发生错误。

知识点

命题的真假判断与应用空间中直线与平面之间的位置关系平面与平面之间的位置关系

1

题型：填空题

|

填空题 · 5 分

15．设函数f (x)的定义域为I，若对x∈I，都有f(x）<x，则称f(x)为T-函数；若对x∈I，都有f[f(x)]<x，则称f(x)为一函数．给出下列命题：

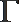
①f (x) =ln(l+x)（x≠0)为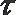-函数；

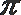
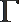
②f (x) =sinx (0<x<)为一函数；

③f (x)为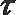-函数是(x)为一函数的充分不必要条件；

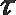
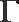
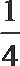
④f (x) =ax2-1既是一函数又是一函数的充要条件是a<一。

其中真命题有．（把你认为真命题的序号都填上）

正确答案

①②④

解析

试题分析：本题属于函数图像的问题，题目的难度较大。注意严格按照题目的定义求解。

考查方向

本题主要考查了函数图像的问题。

解题思路

本题考查函数图像，解题步骤如下：依次画出①②③④中的函数图像，若满足f(x）<x，则称f(x)为T-函数；若有f[f(x)]<x，则称f(x)为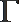一函数．

易错点

本题必须注意严格按照题目的定义求解，忽视则会出现错误。

知识点

充要条件的判定命题的真假判断与应用

1

题型：单选题

|

单选题 · 5 分

3．下列说法中正确的是（）

A“”是“函数是奇函数”的充要条件

B若，则

C若为假命题，则，均为假命题

D命题“若，则”的否命题是“若，则”

正确答案

D

解析

A 错误，既非充分也非必要。原概念：B 错误。C 错误。即p且q是假，只能说明p q中至少一个假，并不能说明都假，所以C错D 正确。注意否命题条件与结论都要否

考查方向

本题主要考查了简易逻辑部分的四个命题的关系，以及真假命题的判定。

解题思路

紧扣定义，逐个判定。

易错点

概念模糊造成失误。

知识点

命题的真假判断与应用

1

题型：单选题

|

单选题 · 5 分

3．设命题p：“若，则”，命题q：“若，则”，则（）

A“”为真命题

B“”为假命题

C“”为假命题

D以上都不对

正确答案

B

解析

若，则或，，故命题为假命题；当，则，故命题为假命题；由真值表可以判定为假命题，为假命题，所以选B选项。

考查方向

本题主要考查了简单命题与复合命题的真假判定，在近几年各省的高考题中出现的频率较高，常与函数的单调性、奇偶性、不等式的性质或解集、立体几何、解析几何、数列、概率等知识交汇命题．

解题思路

1．判定简单命题为假命题，为假命题；

2．由真值表判定复合命题的真假。

易错点

本题易在判定命题的真假时出现错误，易忽视异号的情形。

知识点

命题的真假判断与应用

1

题型：填空题

|

填空题 · 5 分

14．某食品的保鲜时间t（单位：小时）与储藏温度x（单位：）满足函数关系且该食品在的保鲜时间是16小时．

已知甲在某日上午10时购买了该食品，并将其遗放在室外，且此日的室外温度随时间变化如图所示．给出以下四个结论：

①该食品在的保鲜时间是8小时；

②当时，该食品的保鲜时间t随着x增大而逐渐减少；

③到了此日13时，甲所购买的食品还在保鲜时间内；

④到了此日14时，甲所购买的食品已然过了保鲜时间．

其中，所有正确结论的序号是____．

正确答案

①④

解析

因为某食品的保鲜时间t（单位：小时）与储藏温度x（单位：）满足函数关系且该食品在的保鲜时间是16小时．所以，即，解得，所以；因为当时，，所以①正确；因为当时，保鲜时间恒为64小时，当时，该食品的保鲜时间t随着增大而逐渐减少，所以②错误；由图象，得：当到此日12时，温度超过12度，此时的保鲜时间不超过1小时，所以到了此日13时，甲所购买的食品不在保鲜时间内，到了此日14时，甲所购买的食品已然过了保鲜时间;所以③错误,④正确；所以所有正确结论的序号是①④．

考查方向

本题主要考查了命题真假的判定与应用以及函数模型的应用．

解题思路

因为某食品的保鲜时间t（单位：小时）与储藏温度x（单位：）满足函数关系且该食品在的保鲜时间是16小时．所以，即，解得，所以；因为当时，，所以①正确；因为当时，保鲜时间恒为64小时，当时，该食品的保鲜时间t随着增大而逐渐减少，所以②错误；由图象，得：当到此日12时，温度超过12度，此时的保鲜时间不超过1小时，所以到了此日13时，甲所购买的食品不在保鲜时间内，到了此日14时，甲所购买的食品已然过了保鲜时间;所以③错误,④正确；所以所有正确结论的序号是①④．

易错点

本题易在判定在的变换规律时出现错误，易忽视“当时，保鲜时间恒为64小时”。

知识点

命题的真假判断与应用函数的图象

1

题型：单选题

|

单选题 · 5 分

15. 下列四个命题中，

为真命题的是（）

A若，则

B若，则

C若，则

D若，则

正确答案

C

解析

当时，若，则，所以A是错误的；

同向不等式有可加性，而同向相减则不一定成立；

如虽然可得出，但是不能推出，所以B是错误的；

只有同号不等式才具有可倒性，否则不一定成立。如推不出，所以D是错误的。

因为，所以，所以C是正确的。

考查方向

本题主要考查了不等式的基本性质。

解题思路

本题考查了不等式的基本性质，适宜于采用排除法求解。

易错点

本题必须注意讨论字母的取值范围，忽视则会出现错误。

知识点

命题的真假判断与应用不等式的性质

1

题型：单选题

|

单选题 · 5 分

5.已知为两条不同的直线，，为两个不同的平面，下列四个命题：

①，；

②，；

③，；

④，⊥，

其中不正确的有（）

A1个

B2个

C3个

D4个

正确答案

D

解析

因为在四个命题中直线均有可能在平面内，所以都不正确，故选D.

考查方向

本题主要考查了命题真假的判定及空间直线与平面间的位置关系，为高考必考题，在近几年的各省高考题出现的频率较高，常与线面、面面平行垂直的判定定理与性质定理等知识点交汇命题。

解题思路

灵活应用线面、面面平行垂直的判定定理与性质定理逐一进行判断。

易错点

对相关定理的不熟悉导致出错。

知识点

命题的真假判断与应用

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析