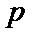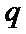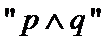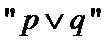- 集合与常用逻辑用语
- 共2295题
15.对于函数
①任取
②函数

③

④函数
⑤若关于x的方程


则其中所有正确结论的序号是_________.(请写出全部正确结论的序号)
正确答案
①②⑤
解析
函数
(1)


(2)如图可知,

(3)
(4)如图所示,函数
(5)若关于x的方程




考查方向
解题思路
先作出图象,则(1),(2),(5)直接通过图象判断;(3)利用特值法判断;(4)函数零点转化成函数图象交点判断
易错点
本题关键是作出图象,正确理解
知识点
4. 命题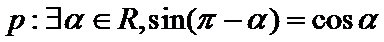
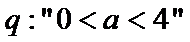
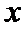
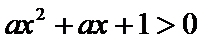
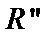
正确答案
解析
对于命题

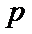
对于命题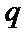


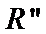
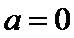
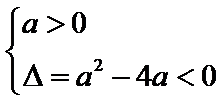
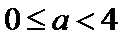
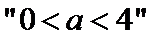
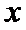
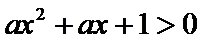
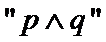
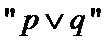
考查方向
解题思路
1.先判断命题p,q的真假;2.利用复合命题真假的判断方法判断即可。
易错点
1.不会判断命题p的真假;2.不知道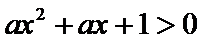
知识点
4.下列说法中正确的是( )
正确答案
解析








考查方向
解题思路
1.奇函数是否过
易错点
本题易在判定命题的否定和否命题时出现错误,以及判断必要条件时出现错误,三角形中角和正弦值之间的关系也易错。
知识点
7.已知函数



正确答案
解析
若命题

(1)当


(2)当




(3)当




综上所述,命题



考查方向
解题思路
1.先分类求解命题

易错点
1.不知道

知识点
下列叙述中正确的是( )
正确答案
考查方向
易错点
1、本题易在充分必要的判断上出问题;
知识点
2.在


正确答案
解析
因为


因为

考查方向
解题思路
先由

易错点
本题易在由

知识点
15.给出下列命题:
① 若函数



② 点


③ 通过回归方程
④ 正弦函数是奇函数,

其中真命题的序号是________.
正确答案
②③
解析
若函数

∴
②③正确;
对于④,正弦函数是奇函数,

故答案为②③.
考查方向
解题思路
对每个命题进行判断,①中根据条件可得函数为周期函数,与对称性无关,②③正确,④中据三角函数的奇偶性,可判断出大前提正确,根据正弦函数的定义,可判断小前提错误.
易错点
无
知识点
以下公式中错误的是_________。
A.资产-负债=净资产
B.以市价计的期初期末净资产差异=储蓄额+未实现资本利得或损失+资产评估增值(-资产评估减值)
C.普通年金终值=每期固定金额×[(1+利率)期限-1]/利率
D.复利现值=终值×(1+利率)期限
正确答案
D
解析
暂无解析
6.对于函数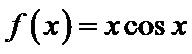
①函数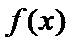
②函数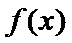
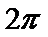
③点

④函数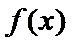
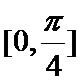
其中是真命题的为( )
正确答案
解析
因为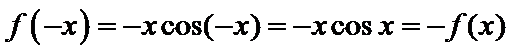
所以函数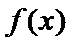
因为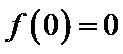
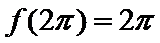
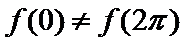
因为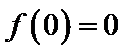
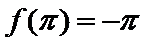
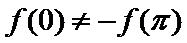
因为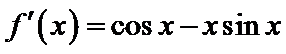
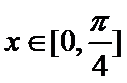
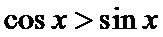
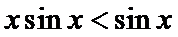
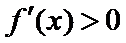
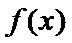
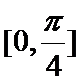
考查方向
解题思路
根据相关知识点逐一进行判断。
易错点
对相关知识不熟悉导致出错。
知识点
某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是
正确答案
考查方向
易错点
本题易看错题目中“错误”二字导致选错。
知识点
6. 下列选项中,说法正确的是( )
正确答案
解析
对于A, 命题“



对于B, 命题“

对于D, 命题“在中


故选C.
考查方向
解题思路
根据命题的四种关系,充分必要条件的定义进行判断即可.
易错点
如果原命题是“若 A则B”,则这个命题的逆命题是“若B则A”,否命题是“若┐A则┐B”,逆否命题是“若┐B则┐A”。这里面有两组等价的命题,即“原命题和它的逆否命题等价,否命题与逆命题等价”。在解答由一个命题写出该命题的其他形式的命题时,一定要明确四种命题的结构以及它们之间的等价关系。另外,在否定一个命题时,要注意全称命题的否定是特称命题,特称命题的否定是全称命题。
知识点
扫码查看完整答案与解析