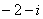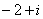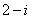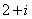集合与常用逻辑用语_章节学习

1

题型：单选题

|

单选题 · 2 分

AA

BB

CC

DD

正确答案

C

知识点

集合的含义

1

题型：单选题

|

单选题 · 2 分

AA

BB

CC

DD

正确答案

D

知识点

集合的含义

1

题型：单选题

|

单选题 · 2 分

AA

BB

CC

DD

正确答案

D

解析

考查方向

考察方向

解题思路

易错点

教师点评

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

1.已知集合，，则AB=（）

A

B[-1,0)

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

若,则复数= ( )

A

B

C

D

正确答案

C

解析

知识点

集合的含义元素与集合关系的判断

1

题型：简答题

|

简答题 · 18 分

23.已知点，平面直角坐标系上的一个动点满足．设动点的轨迹为曲线．

（1）求曲线的轨迹方程；

（2）点是曲线上的任意一点，为圆的任意一条直径，求的取值范围；

（3）已知点是曲线上的两个动点，若(是坐标原点)，试证明：直线与某个定圆恒相切，并写出定圆的方程．

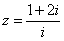
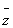
正确答案

见解析。

解析

解析：（1）依据题意，动点满足.

又，

因此，动点的轨迹是焦点在轴上的椭圆，且．

所以，所求曲线的轨迹方程是．

（2）设是曲线上任一点．依据题意，可得．

是直径，

．又，

＝．

由，可得，即．

．

的取值范围是．

（3）证明：因是曲线上满足的两个动点，由曲线关于原点对称，可知直线也关于原点对称．若直线与定圆相切，则定圆的圆心必在原点．因此，只要证明原点到直线的距离()是定值即可．

设，点，则

．

利用面积相等，有，于是．

又两点在曲线上，故可得

因此，．

所以，，即为定值．

所以，直线总与定圆相切，且定圆的方程为：．

知识点

集合的含义

1

题型：简答题

|

简答题 · 14 分

21.有一块铁皮零件，其形状是由边长为的正方形截去一个三角形所得的五边形，其中，如图所示．现在需要用这块材料截取矩形铁皮，使得矩形相邻两边分别落在上，另一顶点落在边或边上．设cm，矩形的面积为．

（1）试求出矩形铁皮的面积关于的函数解析式，并写出定义域；

（2）试问如何截取(即取何值时)，可使得到的矩形的面积最大？

正确答案

见解析。

解析

解析：（1）依据题意并结合图形，可知：

1. 当点在线段上，即时，；

2. 当点在线段上，即时，由，得．

于是，．

所以，定义域．

（2）由（1）知，当时，；

当时，

，当且仅当时，等号成立．

因此，的最大值为．

所以，先在上截取线段，然后过点作的垂线交于点，再过点作的平行线交于点，最后沿与截铁皮，所得矩形面积最大，最大面积为．

知识点

集合的含义

1

题型：简答题

|

简答题 · 18 分

22.已知数列满足，对任意都有．

（1）求数列()的递推公式；

（2）数列满足()，求通项公式；

（3）设，问是否存在实数使得数列()是单调递增数列？若存在，求出的取值范围；若不存在，请说明你的理由．

正确答案

见解析。

解析

解析：（1）对任意都有成立，

∴令，得．

∴数列()的递推公式是

（2）由（1）可知，数列()是首项和公比都为的等比数列，于是．

由()，得

()．

故．

当时，．

所以

（3） ∵，

∴当时，，

，

依据题意，有，即．

当为大于或等于4的偶数时，有恒成立，又随增大而增大，则

，故的取值范围为；

当为大于或等于3的奇数时，有恒成立，故的取值范围为；

当时，由，得．

综上可得，所求的取值范围是．

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上

第Ⅰ卷（选择题）

请点击修改第I卷的文字说明

评卷人

得分

Aa'a'a'a

Bq'q'q'q'q

Cssfs

D q'q'q

正确答案

C

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

1．已知集合，，则＝（）

A

B

C

D

正确答案

A

解析

略

知识点

集合的含义

1

题型：填空题

|

填空题 · 5 分

比较大小：__________.

【年级】高一

正确答案

解析

是上的减函数；

．

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

年至年北京市电影放映场次（单位：万次）的情况如图所示，将年份作为自变量，当年电影放映场次作为函数值，下列函数模型中，最不适合近似描述这年间电影放映场次逐年变化规律的函数是（　　）

A

B

C

D

【年级】高一

正确答案

D

解析

由图象可知在第一象限内，是关于的增函数，A、B、C均合题意

当时，在第一象限内是减函数，

当时，在第一象限内没有图象，

故不适合．

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

已知集合A＝{1，2，3}，B＝{3，4，5，6}，则A∩B＝（　　）

A{3} B．{1，2}

B{4，5，6} D．{1，2，3，4，5，6}

正确答案

A

知识点

集合的含义

1

题型：单选题

|

单选题 · 5 分

【题干】已知全集，集合，则为（）.

A

B{4}

C{0,2,4}

D{0,2,3,4}

正确答案

C

解析

,选C.

知识点

集合的含义

1

题型：单选题

|

单选题 · 123 分

答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效。

参考公式：

若事件A，B互斥，则

若事件A，B相互独立，则

若事件A在一次试验中发生的概率是p，则n次独立重复试验中事件A恰好发生k次的概率

台体的体积公式

其中分别表示台体的上、下底面积，表示台体的高

柱体的体积公式

其中表示柱体的底面积，表示柱体的高

锥体的体积公式

其中表示锥体的底面积，表示锥体的高

球的表面积公式

球的体积公式

其中表示球的半径

选择题部分（共40分）

A1

B2

C3

D4

正确答案

D

知识点

集合的含义

热门试卷

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

教师点评

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

知识点

正确答案

解析

知识点

正确答案

知识点