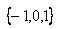- 集合与常用逻辑用语
- 共2295题
设















正确答案
解析
略
知识点
已知集合


正确答案
解析
略
知识点
已知集合

正确答案
解析
略
知识点
若﹁p∨q是假命题,则()
正确答案
解析
略
知识点
已知集合


正确答案
解析
略
知识点
设集合


正确答案
解析
略
知识点
设集合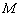
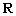
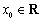
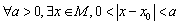
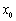
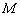

① 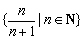
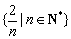
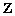
正确答案
解析
略
知识点
已知全集


正确答案
解析
略
知识点
已知集合



正确答案
解析
略
知识点
对于集合





(1)写出


(2)用


(3)有多少个集合对


正确答案
(1)

(2)7
(3)512
解析
(1)解:


(2)
要使









(3)因为
所以
所以
而
所以

所以满足条件的集合对

知识点
定义函数











正确答案
2
解析
略
知识点
对于实数









(1)若

(2)当




(3)若








正确答案
见解析
解析
(1)


所以
(2)


①当



解得

②当



解得

③当



解得

综上,


(3)成立. ………11分
(证明1)
由






①由

②若



则





若

若


但小于

故


从而数列




(证法2,数学归纳法) ………18分
(其它解法可参考给分)
知识点
已知集合


正确答案
解析
略
知识点
已知全集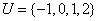
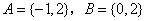
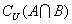
正确答案
解析
略
知识点
已知 









正确答案
解析
解析:若

即当

若

由


即当


由于





故知所求

知识点
扫码查看完整答案与解析