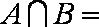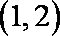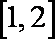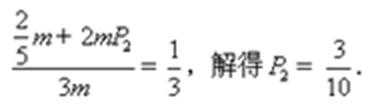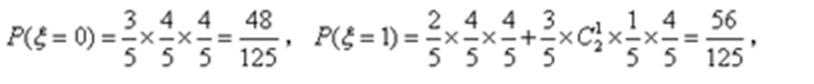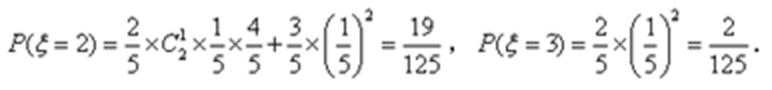- 集合与常用逻辑用语
- 共2295题
在集合
正确答案
解析
解：∵集合
而当n=2和n=10时，
故满足条件
故所取元素恰好满足方程
知识点
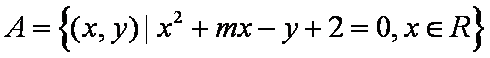
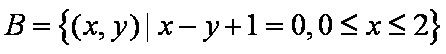
若
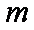
正确答案
见解析
解析
问题等价于方程组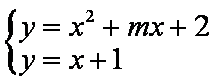
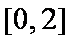
即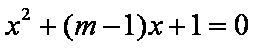
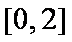
令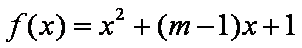
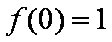
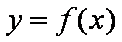
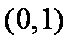
∴抛物线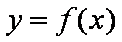
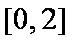
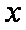
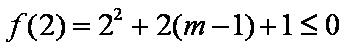
或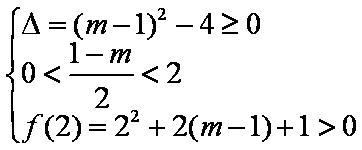
由①得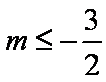
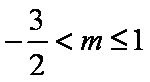
∴实数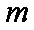
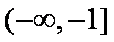
知识点
设集合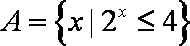
A
B
C[1,2)
D(1,2]
正确答案
解析
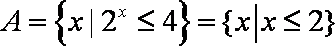
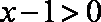
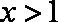
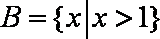
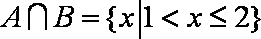
知识点
设集合
A
B
CR
D
正确答案
解析
知识点
已知
（1）求顶点
（2）若线段
正确答案
（1）
解析
解析：（1）因为
由椭圆的定义可知点
所以
（2）由题意可知直线
由
设
又因为
故直线
知识点
已知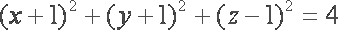
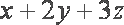
正确答案
解析
由柯西不等式得，
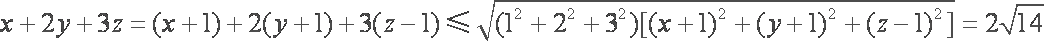
等号当且仅当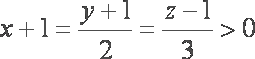
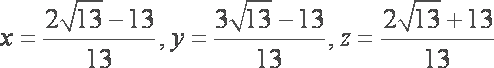
知识点
若全集U＝{1,2,3,4,5,6}，M＝{1,4}，N＝{2,3}，则集合{5,6}等于( )
正确答案
解析
略
知识点
集合A={﹣1，0，1}，B={x|x=m2+1，m∈R}，则A∩B= 。
正确答案
{1}
解析
解：根据题意，集合B={x|x=m2+1，m∈R}={x|x≥1}，
又由集合A={﹣1，0，1}，
则A∩B={1}，
知识点
集合
A
B
C
D
正确答案
解析
由已知条件可得
知识点
已知集合U={﹣1，0，1，2}，A={﹣1，1}，则∁UA= 。
正确答案
{0，2}
解析
解：由U={﹣1，0，1，2}，A={﹣1，1}，
所以∁UA={0，2}。
知识点
设全集U＝R，A＝{x|0.5x>0.25},B={x|y=ln(1-x)}，则
正确答案
解析
A＝{x|x＜2}，B={x|x＜1}，
知识点
某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为
（1）求甲中奖且乙、丙都没有中奖的概率；
（2）求中奖人数ξ的分布列及数学期望Eξ。
正确答案
见解析。
解析
（1）设甲、乙、丙中奖的事件分别为A、B、C，那么
P（A）=P（B）=P（C）=
P（
答：甲中奖且乙、丙都没有中奖的概率为
（2）ξ的可能值为0，1，2，3，
P（ξ=k）=
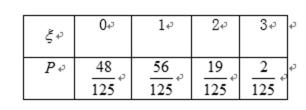
所以中奖人数ξ的分布列为
Eξ=0×
知识点
已知集合A={x||2x﹣1|≤3}，B=（﹣3，a），若A∩B=A，则实数a的取值集合是 。
正确答案
（2，+∞）
解析
∵|2x﹣1|≤3
∴﹣3≤2x﹣1≤3
∴﹣2≤2x≤4
∴﹣1≤x≤2
故A=[﹣1，2]
又∵B=（﹣3，a），
若A∩B=A
则a＞2
故实数a的取值集合是（2，+∞）
知识点
设全集U=R，集合A={x|x≥2}，B={x|0≤x＜5}，则集合（∁UA）∩B=（ ）
正确答案
解析
∵全集U=R，集合A={x|x≥2}
∴CUA={x|x＜2}
∵B={x|0≤x＜5}
∴（CUA）∩B={x|0≤x＜2}
知识点
甲袋和乙袋中都装有大小相同的红球和白球，已知甲袋中共有
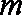
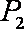
（1）若
（2）若将甲、乙两袋中的球装在一起后，从中摸出1个红球的概率是
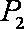
（3）设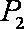
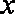
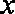
正确答案
见解析
解析
解析：（1）设甲袋中红球的个数为x，依题意得x=10×
（2）由已知得
（3）
所以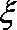
所以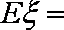
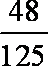
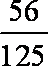
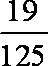
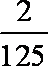
知识点
扫码查看完整答案与解析