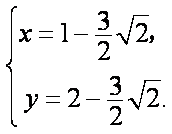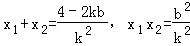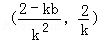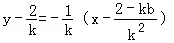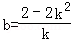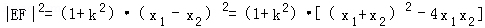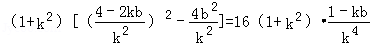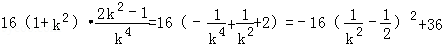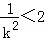- 轨迹方程
- 共25题
14.已知集合








正确答案
2560
解析
解析已在路上飞奔,马上就到!
知识点
14.已知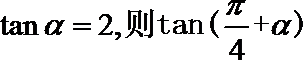

正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
2. 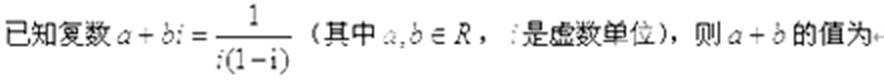
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.若函数




(1)判断函数

(2)若函数



①求证:对任意

②是否对任意

正确答案
(1)函数

例如,当

又
所以,

(2)①假设


则
因为函数

所以,对于任意
即
则
与
所以,对任意的

②不成立.
例如
证明:当


当

所以,函数


即函数

当


所以“对任意

如


解析
解析已在路上飞奔,马上就到!
知识点
9. 方程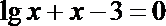
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,…,n,…时,其抛物线在x轴上截得的线段长依次为d1,d2,…,dn,…,则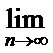
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
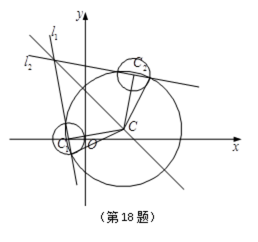
如图,在平面直角坐标系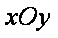
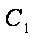
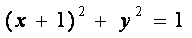
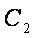
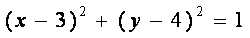
(1)若过点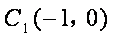
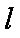
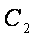
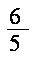
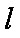
(2)设动圆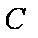
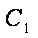
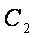
①证明:动圆圆心C在一条定直线上运动;
②动圆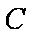
坐标;若不经过,请说明理由。
正确答案
见解析
解析
解:(1)设直线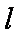
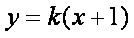

因为直线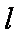
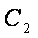
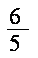
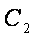
所以圆心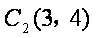
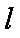

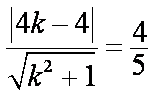
化简,得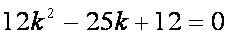
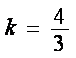
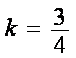
所以直线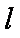
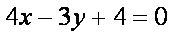
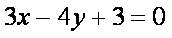
(2)①证明:设圆心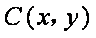
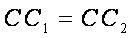
即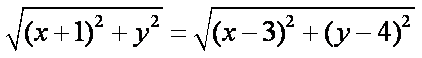
化简得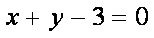
即动圆圆心C在定直线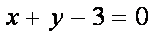
②圆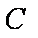
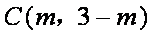
则动圆C的半径为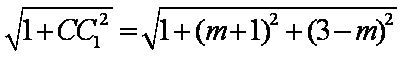
于是动圆C的方程为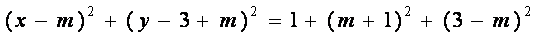
整理,得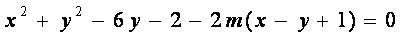
由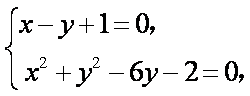
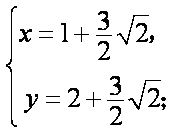
所以定点的坐标为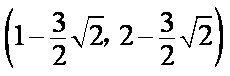
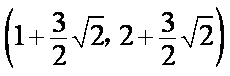
知识点
如图,F1和F2分别是双曲线
正确答案
解析
连接AF1,则∠F1AF2=90°,∠AF2B=60°
∴|AF1|=
|AF2|=

∴
∴e=
故答案为1+
知识点
21.已知定点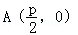
(I)求动点M的轨迹C的方程;
(2)设EF为曲线C的一条动弦(EF不垂直于x轴),其垂直平分线与x轴交于点T(4,0),当p=2时,求|EF|的最大值。
正确答案
(1)y2=2px(p>0,x≠0)
(2)|EF|的最大值为6
解析
如图,
(1)设M(x,y),则BM的中点G的坐标为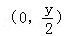
又A(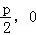
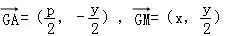
由题意知GA⊥GM,所以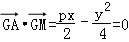
所以y2=2px
当M点在x轴上时不满足题意,故曲线C的方程为y2=2px(p>0,x≠0);
(2)设弦EF所在直线方程为y=kx+b,E(x1,y1),F(x2,y2)
由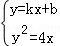
则
则线段EF的中点为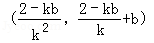
线段EF的垂直平分线方程为
令y=0,x=4,得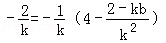
所以
=
=
再由①,△=(2kb﹣4)2﹣4k2b2=4k2b2﹣16kb+16﹣4k2b2=16﹣16kb
=16﹣16(2﹣2k2)=32k2﹣16>0
得: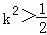
所以,当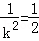
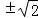
知识点
21.已知函数f(x)=alnx+x2(a为实数).
(Ⅰ)求函数f(x)在区间[1,e]上的最小值及相应的x值;
(Ⅱ)若存在
正确答案
(Ⅰ)解:f(x)=alnx+x2的定义域为(0,+∞),f′(x)=

当x

若a≥-2,f′(x)在[1,e]上非负(仅当a=-2,x=-1时,f′(x)=0),
故f(x)在[1,e]上单调递增,此时f(x)min=f(1)=1;
若-2e2<a<-2,令f′(x)<0,解得1≤x<
令f′(x)>0,解得
∴f(x)min=f(

若a≤-2e2,f′(x)在[1,e]上非正(仅当a=-2e2,x=e时,f′(x)=0),
故f(x)在[1,e]上单调递减,此时f(x)min=f(e)=a+e2.
综上所述,得a≥-2时,f(x)min=1,相应的x=1;
当-2e2<a<-2时,f(x)min=

当a≤-2e2时,f(x)min=a+e2,相应的x=e.
(Ⅱ)解:不等式f(x)≤(a+2)x可化为a(x-lnx)≥x2-2x.
∵x
因而a≥

令g(x)=


当x
从而g′(x)≥0(仅当x=1时取等号),∴g(x)在[1,e]上是增函数,
故g(x)min=g(1)= -1,∴实数a的取值范围是[-1,+∞).
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析