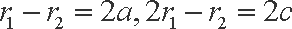双曲线及其性质
共531题

双曲线及其性质
共531题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知曲线:和:，且曲线的焦点分别为、，点是和的一个交点，则△的形状是（）

A锐角三角形

B直角三角形

C钝角三角形

D都有可能

正确答案

解析

直角三角形

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

已知F2、F1是双曲线-=1(a>0，b>0)的左右焦点F2关于渐近线的对称点恰好落在以F1为圆心，|OF1|为半径的圆上，则双曲线的离心率为

正确答案

解析

画出图形根据双曲线的性质和圆的有关知识可以得到，故选C.

知识点

双曲线的定义及标准方程

题型：简答题

简答题 · 12 分

已知函数在点处的切线方程为 .

（1）求函数的解析式；

（2）若过点可作曲线的三条切线，求实数的取值范围。

正确答案

见解析

解析

（1）。

根据题意，得即解得

所以

（2）因为点不在曲线上，所以可设切点为。

则。

因为，所以切线的斜率为。

则=，

即。

因为过点可作曲线的三条切线，

所以方程有三个不同的实数解。

所以函数有三个不同的零点。

则，令，则或。

则，即，

解得。

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

若双曲线的左、右顶点分别为，点是第一象限内双曲线上的点，若直线的倾斜角分别为，且，那么的值是（）

正确答案

解析

∵双曲线的方程为，，∴双曲线的左顶点为，右顶点为，设，得直线的斜率，直线的斜率，∴①，∵是双曲线上的点，∴，得，代人①式得，∵直线的倾斜角分别为，所以，∴，∵是第一象限内双曲线上的点，易知均为锐角，∴，解得，故选D。

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

点P在双曲线上，是这条双曲线的两个焦点，，且的三条边长成等差数列，则此双曲线的离心率是（　　　）

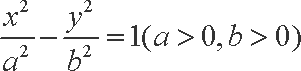
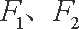
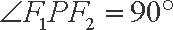
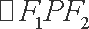
正确答案

解析

不妨设点P在双曲线的左支上，设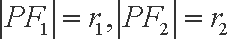，则

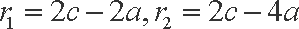
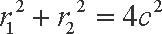
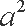
解得，又代入两边同除以得

解得，，故选D。

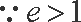
知识点

双曲线的定义及标准方程

题型：简答题

简答题 · 13 分

已知椭圆过点，且离心率.

（1）求椭圆的方程；

（2）已知过点的直线与该椭圆相交于、两点，试问：在直线上是否存在点，使得是正三角形？若存在，求出点的坐标；若不存在，请说明理由。

正确答案

见解析

解析

（1）由题意得………………2分

解得………………4分

所以椭圆的方程为……………… 5分

（2）当直线的斜率为0或不存在时，不存在符合题意的点；………………6分

当直线的斜率存在且不为0时，设直线的方程为

代入，整理得

设，，则，

设存在符合题意的点，

则

…………8分

设线段的中点，则，所以

因为是正三角形，所以且，即

……………9分

由得即，所以

所以

……………10分

由得，

解得，所以………………12分

由得

所以

所以存在符合题意的点………………13分

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

设双曲线的右焦点为，过点作与轴垂直的直线交两渐近线于、两点，与双曲线的其中一个交点为，设为坐标原点，若，且，则该双曲线的离心率为

B‍

C‍‍

正确答案

解析

‍，代入，得，代入双曲线方程，得，即可得；

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

已知双曲线的焦距为，焦点到一条渐近线的距离为，则双曲线的标准方程为

C或

D或

正确答案

解析

由题易知，故，这样的双曲线标准方程有两个。

知识点

双曲线的定义及标准方程

题型：简答题

简答题 · 12 分

如图，在四棱锥P-ABCD中，PA丄平面ABCD, ，,AD=AB=1,AC 和 BD 交于O点。

（1）求证：平面PBD丄平面PAC

（2）当点A在平面PBD内的射影G恰好是ΔPBD的重心时，求二面角B-PD-G的余弦值.

正确答案

见解析

解析

解析：（1）依题意，，，所以，……2分

而面，，又，∴面，

又面，∴平面平面…………4分

（2）过作的垂线为轴，为轴，为轴，建立如图所示坐标系，

则，，,设，

所以，，

由，得

解得，.………………6分

∴P点的坐标为；

面的一个法向量为，……………8分

设面的一个法向量为，，

即，∴ ………………10分

，

所以二面角的余弦值为，……………12分

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

过双曲线﹣=1（a＞0，b＞0）的左焦点F（﹣c，0）（c＞0），作倾斜角为的直线FE交该双曲线右支于点P，若=（+），且•=0则双曲线的离心率为（　　）

正确答案

解析

在Rt△PFF′中，OE=OF=c。

∵=（+），

∴E为PF的中点，令右焦点为F′，则O为FF′的中点，

则PF′=2OE=c，

∵•=0，

∴OE⊥PF

∴PF′⊥PF

∵PF﹣PF′=2a

∴PF=PF′+2a=2a+c

在Rt△PFF′中，PF2+PF′2=FF′2

即（2a+c）2+c2=4c2

⇒所以离心率e==+1。

知识点

双曲线的定义及标准方程

继续学习学习下一知识点

下一知识点 : 抛物线及其性质

百度题库 > 高考 > 理科数学 > 双曲线及其性质

扫码查看完整答案与解析